[게임 수학] Chapter 17. 캐릭터: 게임에 생기를 불어넣는 기술
Table of Contents
이득우의 게임 수학 책을 읽고 공부한 노트입니다.
스켈레탈 애니메이션 #
- 스켈레탈 애니메이션(Skeletal animation)
- 가상의 뼈대인 본(Bone) 을 캐릭터 메시에 심은 후, 이 본의 움직임에 맞춰서 캐릭터 메시를 변형시켜 애니메이션을 구현하는 방식이다.
- 본의 정보를 메시에 추가하면, 메시는 본이 있는 메시(스킨드 메시: Skinned mesh) 와 본이 없는 메시로 나뉘게 된다.
- 본은 다음과 같은 정보들이 필요하다.
- (1) 본을 식별할 고유한 이름 정보
- (2) 본의 트랜스폼 정보 (크기, 회전, 이동이 가능하므로, 트랜스폼이 필요하다)
- (3) 본의 처음 배치 정보 : 바인드 포즈(Bindpose)
enum class MeshType : UINT32
{
Normal = 0,
Skinned
};
class Bone
{
private:
std::size_t _Hash = 0;
std::string _Name;
Transform _Transform;
Transform _Bindpose;
};
- 리깅(Rigging)
- 본과 정점을 연결하는 작업이다.
- 즉, 하나의 정점에 어떤 본들이 얼마나 영향을 미치는지 기록하는 것이다.
- 여기서 한 정점에 영향을 주는 본들의 연결 정보를 웨이트(Weight) 라고 한다.
struct Weight
{
std::vector<std::string> Bones; // 어떤 본들이
std::vector<float> Values; // 얼마나 영향을 주는지
};
-
Chapter 8에서 보았던 메시 정보를 스킨드 메시로 확장하고 리깅 정보를 추가하면 다음과 같이 되겠다.
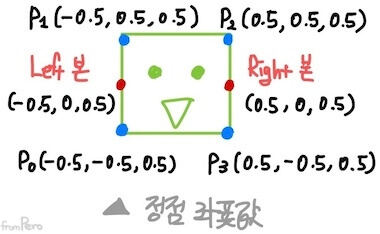
-
정점 버퍼
순서 좌표 UV 좌표 연결된 본의 수 연결 정보 0 (-0.5, -0.5, 0.5) (0.125, 0.75) 1 Left, 1 1 (-0.5, 0.5, 0.5) (0.125, 0.875) 1 Left, 1 2 (0.5, 0.5, 0.5) (0.25, 0.75) 1 Right, 1 3 (0.5, -0.5, 0.5) (0.25, 0.875) 1 Right, 1 -
인덱스 버퍼
순서 삼각형 정점 순서 0 0 0 1 0 1 2 0 2 3 1 0 4 1 2 5 1 3 -
본 목록
이름 좌표 Left (-0.5, 0, 0.5) Right (0.5, 0, 0.5)
bool GameEngine::LoadResources()
{
// 사각 메시
// ...
// 스킨드 메시로 설정한다.
quadMesh.SetMeshType(MeshType::Skinned);
auto& bones = quadMesh.GetBones();
auto& connectedBones = quadMesh.GetConnectedBones();
auto& weights = quadMesh.GetWeights();
// 본 정보를 설정한다.
bones = {
{"left", Bone("left", Transform(Vector3(-1.f, 0.f, 0.f) * halfSize))},
{"right", Bone("right", Transform(Vector3(1.f, 0.f, 0.f) * halfSize))}
};
// 4개의 정점은 본이 각각 1개씩 연결되어 있다.
connectedBones = { 1, 1, 1, 1 };
// 정점마다의 본 이름과 가중치를 설정한다.
weights = {
{ {"left"}, {1.f} },
{ {"left"}, {1.f} },
{ {"right"}, {1.f} },
{ {"right"}, {1.f} }
};
// ...
}
- 게임 엔진은 애니메이션을 시간에 따라 변환된 값을 얻기 위해 키프레임(Keyframe) 데이터를 사용한다.
- 주요 지점에 점을 찍어서 값을 지정하면, 나머지 값들은 보간을 통해 끊기지 않는 데이터를 제공한다.
- 게임 로직과 본의 움직임 중 어떤 것을 먼저 처리해야 할까?
- 게임 로직 결과에 맞는 적절한 애니메이션을 렌더링하기 위해서는
- (1) 게임 로직이 완료된 후 (
Update3D) - (2) 애니메이션 로직으로 본의 위치를 설정하고 (
LateUpdate3D) - (3) 렌더링 해야할 것이다. (
Render3D)
- 애니메이션 로직을 구현하면 다음과 같다.
// 애니메이션 로직 : 본의 위치를 설정
void SoftRenderer::LateUpdate3D(float InDeltaSeconds)
{
GameEngine& g = Get3DGameEngine();
static float duration = 3.f;
static float elapsedTime = 0.f;
// 애니메이션을 위한 커브 생성
// 시간에 따라 [0, 1]범위의 사인 파형을 생성하고 본을 움직이는 데 사용한다.
// (키프레임 데이터를 대체하기 위해 간단하게 sin 곡선을 사용했다.)
// elapsedTime은 시간에 따라 0~3의 값이 나온다.
elapsedTime = Math::Clamp(elapsedTime + InDeltaSeconds, 0.f, duration);
if (elapsedTime == duration)
{
elapsedTime = 0.f;
}
// 0~360 사이의 값으로 대응시킨다.
float sinParam = elapsedTime / duration * Math::TwoPI ;
// -1~1 사이의 sin 결과 값을 0~1 사이의 값으로 대응시킨다.
float sinWave = (sinf(sinParam) + 1.f) * 0.5f;
// 스킨드 메시가 아니면 종료한다.
GameObject& goPlayer = g.GetGameObject(PlayerGo);
Mesh& m = g.GetMesh(goPlayer.GetMeshKey());
if (!m.IsSkinnedMesh())
{
return;
}
const std::string leftBoneName("left");
const std::string rightBoneName("right");
Transform& leftBoneTransform = m.GetBone(leftBoneName).GetTransform();
Transform& rightBoneTransform = m.GetBone(rightBoneName).GetTransform();
// 기준 위치에서 추가로 움직인 본의 위치를 계산한다.
Vector3 deltaLeftPosition = Vector3::UnitX * -sinWave;
Vector3 deltaRightPosition = Vector3::UnitX * sinWave;
// 본의 바인드 포즈(최초 위치)를 기준으로 변경된 위치를 더해서 최종 위치를 계산한다.
leftBonePosition = m.GetBindPose(leftBoneName).GetPosition() + deltaLeftPosition;
rightBonePosition = m.GetBindPose(rightBoneName).GetPosition() + deltaRightPosition;
// 최종 위치를 설정한다.
leftBoneTransform.SetPosition(leftBonePosition);
rightBoneTransform.SetPosition(rightBonePosition);
}
- 정점 버퍼의 데이터를 행렬로 곱하기 전에, 본의 움직임을 반영해서 최종 위치를 계산해야 하겠다.
// 메시를 그리는 함수
void SoftRenderer::DrawMesh3D(const Mesh& InMesh, const Matrix4x4& InMatrix, const LinearColor& InColor)
{
size_t vertexCount = InMesh.GetVertices().size();
size_t indexCount = InMesh.GetIndices().size();
size_t triangleCount = indexCount / 3;
std::vector<Vertex3D> vertices(vertexCount);
std::vector<size_t> indice(InMesh.GetIndices());
for (size_t vi = 0; vi < vertexCount; ++vi)
{
vertices[vi].Position = Vector4(InMesh.GetVertices()[vi]);
// 정점 변환 전에, 본의 움직임을 반영한다.
if (InMesh.IsSkinnedMesh())
{
Vector4 totalPosition = Vector4::Zero;
Weight w = InMesh.GetWeights()[vi];
// 메시에 연결된 본의 개수에 따라 반복
for (size_t wi = 0; wi < InMesh.GetConnectedBones()[vi]; ++wi)
{
std::string boneName = w.Bones[wi];
if (InMesh.HasBone(boneName) == false) continue;
const Transform& boneTransform = InMesh.GetBone(boneName).GetTransform();
// 본 - 바인드포즈 = 바인드 포즈로부터의 상대적 위치
Vector3 deltaPosition = boneTransform.GetPosition() - InMesh.GetBindPose(boneName).GetPosition();
// 상대적 위치에 웨이트 값을 적용시킨다.
totalDeltaPosition += deltaPosition * w.Values[wi];
}
// 정점 위치에 반영한다.
vertices[vi].Position += Vector4(totalDeltaPosition, false);
}
if (InMesh.HasColor())
{
vertices[vi].Color = InMesh.GetColors()[vi];
}
if (InMesh.HasUV())
{
vertices[vi].UV = InMesh.GetUVs()[vi];
}
}
// 정점 변환 진행
VertexShader3D(vertices, InMatrix);
// 삼각형 별로 그리기
// ....
}
트랜스폼 계층 구조 #
- 일반적으로 캐릭터를 구성하는 본은 부모-자식 관계의 계층 구조가 형성되어 있다. 그래서 부모가 움직이면 자식들도 움직이게 된다.
- 부모가 없는 최상단의 트랜스폼을 루트(Root) 트랜스폼이라고 한다.
- 이런 계층 구조에 따라서 트랜스폼 데이터는 다음과 같이 나뉠 수 있다.
이름 설명 로컬(local) 트랜스폼
상대(relative) 트랜스폼부모로부터 상대적인 트랜스폼 월드(world) 트랜스폼
절대(absolute) 트랜스폼(계층 구조와 상관없이)
자신이 속한 공간에서의 트랜스폼
class TransformComponent
{
public:
bool SetRoot();
TransformComponent& GetRoot();
bool SetParent(TransformComponent& InTransform);
private:
// 부모와 자식 목록을 보관한다.
TransformComponent* _ParentPtr = nullptr;
std::vector<TransformComponent*> _ChildrenPtr;
// 매번 월드 트랜스폼을 로컬 트랜스폼으로 계산해 주기 보다는
// 두 가지 트랜스폼을 모두 보관해 놓으면 좋겠다.
Transform _LocalTransform;
Transform _WorldTransform;
};
트랜스폼 계층 구조의 변환 #
- 부모나 자식의 트랜스폼 값이 변경되면 관련된 트랜스폼 값들을 조정해줘야 할 것이다. 사례를 통해 어떤 연산이 필요한지 알아보자.
- 사례 1. 부모의 월드 트랜스폼 변경 시
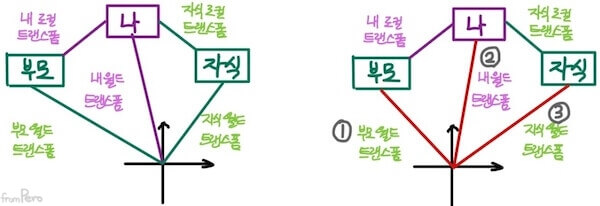
- 사례 2. 나의 로컬 트랜스폼 변경 시
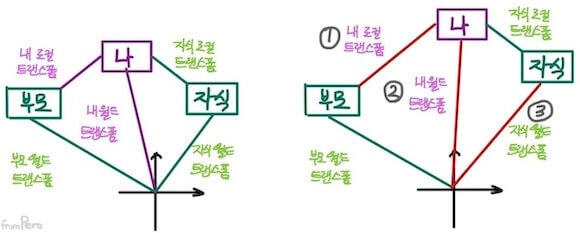
- 사례 3. 나의 월드 트랜스폼 변경 시
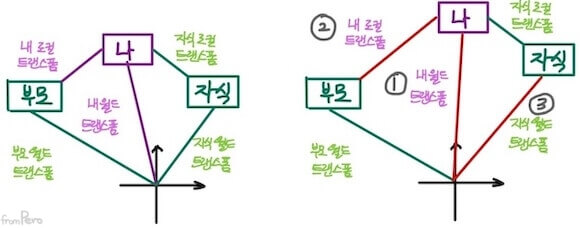
- 사례 4. 새로운 부모 설정 시
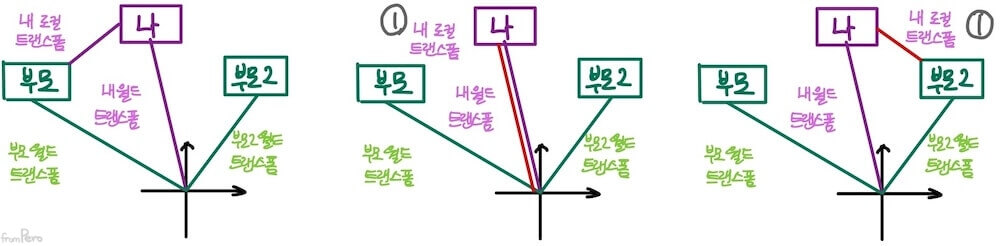
- 위와 같은 사례들을 통해 다음과 같은 두 가지 기능이 필요함을 알 수 있다.
- (1) 부모의 월드 트랜스폼 정보, 나의 로컬 트랜스폼 정보 → 나의 월드 트랜스폼 계산
- (2) 부모의 월드 트랜스폼 정보, 나의 월드 트랜스폼 정보 → 나의 로컬 트랜스폼 계산
(1) 로컬 트랜스폼으로부터 월드 트랜스폼의 계산 #
- 내 월드 트랜스폼의 크기
- 부모 월드 트랜스폼의 크기 $\vec{s}$와 내 로컬 트랜스폼의 크기 $\vec{s’}$를 곱하면 된다. $$\vec{s’_{world}} = \vec{s} * \vec{s’}$$
- 내 월드 트랜스폼의 회전
- 부모 월드 회전 사원수 $q$와 나의 로컬 회전 사원수 $q’$을 곱하면 된다. $$q’_{world} = q’ * q $$
- 내 월드 트랜스폼의 이동
- 내 월드 트랜스폼의 모델링 행렬은 다음과 같을 것이다. $$M_{world} = M_{parnet} \cdot M_{local}$$ $$ M_{world} = \begin{bmatrix} x_xs_x & y_xs_y & z_xs_z & t_x \\ x_ys_z & y_ys_y & z_ys_z & t_y \\ x_zs_x & y_zs_y & z_zs_z & t_y \\ s_zs_x & y_zs_y & z_zs_z & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x’_xs’_x & y’_xs’_y & z’_xs’_z & t’_x \\ x’_ys’_z & y_ys’_y & z’_ys’_z & t’_y \\ x’_zs’_x & y’_zs’_y & z’_zs’_z & t’_y \\ s’_zs’_x & y’_zs’_y & z’_zs’_z & t’_z \\ 0 & 0 & 0 & 1 \end{bmatrix} $$
- 이것의 4열만 월드 이동 값이므로 4열만 내적과 곱셈으로 정리하자. $$ \vec{t_{world}} = (\begin{bmatrix} x_x & y_x & z_x \\ s_y & y_y & z_y \\ x_z & y_z & z_z \end{bmatrix} \begin{bmatrix} t’_x \\ t’_y \\ t’_z \end{bmatrix} ) * \vec{s} + \vec{t} $$ $$ = (q \cdot \vec{t’} ) * \vec{s} + \vec{t} $$
// 로컬 트랜스폼 -> 월드 트랜스폼
FORCEINLINE constexpr Transform Transform::LocalToWorld(const Transform& InParentWorldTransform) const
{
Transform result;
// 크기
result.SetScale(InParentWorldTransform.GetScale() * GetScale());
// 회전
result.SetRotation(InParentWorldTransform.GetRotation() * GetRotation());
// 이동
result.SetPosition(InParentWorldTransform.GetPosition() + InParentWorldTransform.GetRotation() * (InParentWorldTransform.GetScale() * GetPosition()));
return result;
}
(2) 월드 트랜스폼으로부터 로컬 트랜스폼의 계산 #
- 먼저 부모의 월드 트랜스폼을 중심으로 나의 월드 트랜스폼을 해석해야 한다.
- 이것은 Chapter 10에서 월드 공간에서 카메라 공간으로 중심을 바꾼 것과 유사하다.
- 따라서 부모의 월드 트랜스폼에 역변환을 한 후에 나의 월드 트랜스폼을 곱하면 나의 로컬 트랜스폼이 만들어질 것이다.
- 부모의 월드 트랜스폼을 역변환해보자.
- 부모의 월드 트랜스폼의 크기의 역변환 $$ \vec{s^{-1}} = (\frac{1}{s_x}, \frac{1}{s_y}, \frac{1}{s_z}) $$
- 부모의 월드 트랜스폼의 회전의 역변환
- 켤레 사원 수 $ q^* $가 된다.
- 부모의 월드 트랜스폼의 이동의 역변환
- 부모 월드 트랜스폼의 모델링 행렬의 역행렬은 다음과 같을 것이다. $$ M^{-1} = (TRS)^{-1} = S^{-1}R^{-1}T^{-1} $$
- 이것을 정리하면 다음과 같다. $$ \vec{t^{-1}} = (\begin{bmatrix} x_x & x_y & x_z \\ y_x & y_y & y_z \\ z_x & z_y & z_z \end{bmatrix} \begin{bmatrix} -t_x \\ -t_y \\ -t_z \end{bmatrix} ) * \vec{s^{-1}} $$ $$ = (q^* \cdot -\vec{t} ) * \vec{s^{-1}} $$
FORCEINLINE constexpr Transform Transform::Inverse() const
{
Vector3 reciprocalScale = Vector3::Zero;
Transform result;
// 크기
// 트랜스폼 크기 값에 0이 있을 수도 있으므로
// 이럴 때는 안전하게 역수로 구성된 벡터를 사용한다.
if (!Math::EqualsInTolerance(Scale.X, 0.f)) reciprocalScale.X = 1.f / Scale.X;
if (!Math::EqualsInTolerance(Scale.Y, 0.f)) reciprocalScale.Y = 1.f / Scale.Y;
if (!Math::EqualsInTolerance(Scale.Z, 0.f)) reciprocalScale.Z = 1.f / Scale.Z;
result.SetScale(reciprocalScale);
// 회전
result.SetRotation(Rotation.Inverse());
// 이동
result.SetPosition(result.GetScale() * (result.GetRotation() * -Position));
return result;
}
- 이제 역변환을 구한 것에 나의 월드 트랜스폼을 곱하면 나의 로컬 트랜스폼이 만들어진다. $$ M_{local} = M_{parent}^{-1} \cdot M_{world} $$
- 내 로컬 트랜스폼의 크기
- 부모 월드 트랜스폼의 크기 역변환 $\vec{s^{-1}}$와 내 월드 트랜스폼의 크기 $\vec{s’}$를 곱하면 된다. $$\vec{s’_{local}} = \vec{s^{-1}} * \vec{s’}$$
- 내 로컬 트랜스폼의 회전
- 내 월드 회전 사원수 $q’$와 부모의 월드 회전 사원수 역변환 $q^*$을 곱하면 된다.
$$q’_{local} = q^* * q’ $$
- 내 월드 회전 사원수 $q’$와 부모의 월드 회전 사원수 역변환 $q^*$을 곱하면 된다.
- 내 월드 트랜스폼의 이동
- 이전 식을 참고해서 구하면 다음과 같다. $$ \vec{t’_{local}} = (q^* \cdot \vec{t’}) * \vec{s^{-1}} + \vec{t^{-1}} $$
// 월드 트랜스폼 -> 로컬 트랜스폼
FORCEINLINE constexpr Transform Transform::WorldToLocal(const Transform& InParentWorldTransform) const
{
// 부모 트랜스폼의 역변환 구하기
Transform invParent = InParentWorldTransform.Inverse();
Transform result;
// 크기
result.SetScale(invParent.GetScale() * GetScale());
// 회전
result.SetRotation(invParent.GetRotation() * GetRotation());
// 이동
result.SetPosition(invParent.GetPosition() + (invParent.GetRotation() * (invParent.GetScale() * GetPosition())));
return result;
}
- 다음은 캐릭터의 바인드 포즈 트랜스폼을 사용해서 애니메이션으로 움직인 본의 변화량을 반영해 최종 정점 위치를 계산하는 코드이다.
// 메시를 그리는 함수
void SoftRenderer::DrawMesh3D(const Mesh& InMesh, const Matrix4x4& InMatrix, const LinearColor& InColor)
{
size_t vertexCount = InMesh.GetVertices().size();
size_t indexCount = InMesh.GetIndices().size();
size_t triangleCount = indexCount / 3;
std::vector<Vertex3D> vertices(vertexCount);
std::vector<size_t> indice(InMesh.GetIndices());
for (size_t vi = 0; vi < vertexCount; ++vi)
{
vertices[vi].Position = Vector4(InMesh.GetVertices()[vi]);
// 정점 변환 전에, 본의 움직임을 반영한다.
if (InMesh.IsSkinnedMesh())
{
Vector4 totalPosition = Vector4::Zero;
Weight w = InMesh.GetWeights()[vi];
// 해당 정점에 연결된 본의 개수에 따라 반복한다.
for (size_t wi = 0; wi < InMesh.GetConnectedBones()[vi]; ++wi)
{
std::string boneName = w.Bones[wi];
if (InMesh.HasBone(boneName) == false) continue;
const Bone& b = InMesh.GetBone(boneName);
const Transform& t = b.GetTransform().GetWorldTransform();
const Transform& bindPose = b.GetBindPose();
// 바인드 포즈를 중심으로 본의 로컬 트랜스폼을 계산한다.
Transform boneLocal = t.WorldToLocal(bindPose);
// 바인드 포즈를 중심으로 정점의 로컬 좌표를 얻는다.
Vector3 localPosition = bindPose.WorldToLocalVector(vertices[vi].Position.ToVector3());
// 본의 로컬 트랜스폼 행렬 * 정점의 로컬 좌표 = 바인드포즈에서 변화된 좌표 계산
Vector3 skinnedLocalPosition = boneLocal.GetMatrix() * localPosition;
// 바인드 포즈의 행렬 * 바인드포즈에서 변화된 좌표 = 모델링 공간으로 되돌리기
Vector3 skinnedWorldPosition = bindPose.GetMatrix() * skinnedLocalPosition;
// 가중치를 반영한 후, 최종 위치에 누적시킨다.
totalPosition += Vector4(skinnedWorldPosition, true) * w.Values[wi];
}
// 정점 위치에 반영한다.
vertices[vi].Position = totalPosition;
}
if (InMesh.HasColor())
{
vertices[vi].Color = InMesh.GetColors()[vi];
}
if (InMesh.HasUV())
{
vertices[vi].UV = InMesh.GetUVs()[vi];
}
}
// 정점 변환 진행
VertexShader3D(vertices, InMatrix);
// 삼각형 별로 그리기
// ...
}