[Game Math] Chapter 15. 오일러 공식: 허수로 표현하는 회전 변환

Table of Contents

이득우의 게임 수학 책을 읽고 공부한 노트입니다.

자연지수함수 #

무리수 e #

스위스 수학자 야코프 베르누이(Jakob Bernouli)는 아래 수식으로 복리 수익을 연구하고 있었다. $$y = (1+ \frac{1}{x})^x$$
- 그러다가 굉장히 큰 값을 $x$에 대입할 수록 결괏값이 특정 상수 $2.7182818…$에 근접한다는 사실을 알아냈다.
- 이 수를 무리수 $e$라고 부른다.

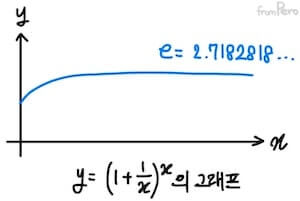
무리수 $e$를 극한(Limit)과 무한대($\infty$)의 개념을 사용해서 다음과 같이 표현할 수 있다. $$e = \lim_{x \to \infty} (1+ \frac{1}{x})^x$$
수렴한다(Converge)
- 극한의 결괏값이 특정 값에 한없이 가까워지면 이를 어떤 값에 수렴한다고 표현한다.
발산한다(Diverge)
- 극한의 결괏값이 무한대로 증가하거나 여러 값을들 오고가면 발산한다고 표현한다.

자연지수함수 #

거듭제곱(Exponentiation) $$3^5 = 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3$$
- 같은 수를 여러번 곱하는 작업이다.
지수(Exponent)
- 곱하는 횟수
- 위 예시에서 $5$
밑(Base)
- 곱하는 수
- 위 예시에서 $3$

지수법칙(Law of exponents) $$ a^m \cdot a^n = a^{m+n} $$ $$ (a^m)^n = a^{m \cdot n} $$ $$ a^0 = 1 $$

지수함수(Exponential function) $$ f(x) = a^x $$
- 지수 법칙에 따라 지수함수의 $x$가 $0$이면, 출력은 항상 $0$이다. 따라서 이 함수는 늘 좌표 $(0, 1)$을 지난다.
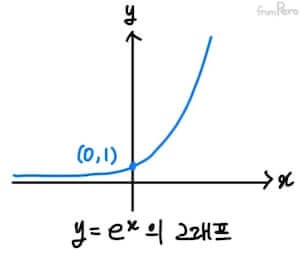
자연지수함수(Natural exponential function) $$ f(x) = e^x $$
- 밑이 무리수 $e$인 지수함수이다.
- 언제나 $(0, 1)$을 지나며, 아래 그래프와 같이 $x$가 커질 수록 급격히 증가하는 형태이다.

미분 #

미분(Differentiation)
- 미분 가능한 함수를 대상으로, 특정 지점에서의 접선의 기울기를 측정하는 작업이다.
- 여기서 살펴볼 자연지수함수, $\sin$함수, $\cos$함수 모두 미분 가능한 함수이다.

할선(Secant line)
- 곡선과 직선이 두 점에서 만날 때의 직선.
- 어떤 미분 가능한 함수가 주어졌을 때, $x$가 $a$일 때와 $b$일 때 대응 되는 두 좌표를 연결하면 할선이 생긴다.
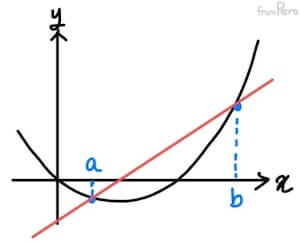
- 이때 할선의 기울기는 다음과 같이 구할 수 있다. $$ m = \frac{f(b) - f(a)}{b - a} $$
- 여기서 $a$는 고정하고, $b$를 $a$쪽으로 서서히 이동시켜보자.
- $b$가 $a$에 한없이 가까워지면, 마치 $a$ 지점에서의 기울기처럼 보일 것이다.
접선(Tangent line)
- 곡선과 직선이 한 점에서 만날 때의 직선.
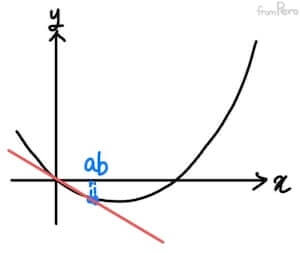
- 이렇게 한없이 가까워지는 개념을 사용해서 특정 지점에서의 기울기를 나타내는 접선을 만들 수 있다.

극한의 개념을 사용해서 기울기 $m$을 구하면 다음과 같다. $$ m = \lim_{b \to a} \frac{f(b) - f(a)}{b - a} $$
- 여기서 $b$는 $a$에다가 한없이 작은 값인 $h$를 더한 것과 같다. 따라서 아래와 같이 바꿔볼 수 있겠다.
미분 계수(Differential coefficient) $$ m = \lim_{h \to 0} \frac{f(a + h) - f(a)}{h} $$
- 주어진 값에 대한 접선의 기울기이다.
- 위 식은 $a$에서의 미분 계수라고 볼 수 있다.

도함수 #

도함수(Derivative) $$ f’(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} $$
- 임의의 수 $x$에 대한 미분 계수를 구할 수 있도록 일반화한 함수이다.
- 보통 미분이라고 부르며 $f’(x)$로 표현한다.
- 이 식을 가지고, 자연지수함수, $\sin$함수, $\cos$함수에 대한 도함수를 계산할 수 있다.

상수함수 $$ f(x) = c $$
- 정의역과 무관하게 항상 일정한 값을 가지는 함수이다.
- 도함수 계산식에 대입하면, 그 결과값은 언제나 $0$이 된다. 이것은 상수함수의 모든 $x$에 대한 접선의 기울기가 $0$이라는 것을 뜻한다.

극한의 여섯 가지 성질
- (1) 두 함수 합의 극한값 = 각 극한값의 합 $$ \lim_{x \to a} [f(x) + g(x)] = \lim_{x \to a}f(x) + \lim_{x \to a}g(x) $$
- (2) 상수와 함수 곱의 극한값 = 함수 극한값과 상수의 곱 $$ \lim_{x \to a} cf(x) = c \lim_{x \to a} f(x) $$
- (3) 두 함수 곱의 극한값 = 각 극한값의 곱 $$ \lim_{x \to a} [f(x) \cdot g(x)] = \lim_{x \to a} f(x) \cdot \lim_{x \to a} g(x) $$
- (4) 두 함수 나눗셈의 극한값 = 각 극한값의 나눗셈 (단, 분모의 극한값은 $0$이 아니어야 함) $$ \lim_{x \to a} [\frac{f(x)}{g(x)}] = \frac{\lim_{x \to a}f(x)}{\lim_{x \to a}g(x)} $$
- (5) 함수를 거듭제곱한 극한값 = 극한값을 거듭제곱한 값 $$ \lim_{x \to a} [f(x)]^n = [\lim_{x \to a} f(x)]^n $$
- (6) 조임 정리(Squeeze theorem)
  - 세 함수의 대소관계에서 양 끝의 극한값이 같다면, 가운데 극한값도 같다.
  - $ g(x) \leq f(x) \leq h(x) $에서 $\lim_{x \to a} g(x) = \lim_{x \to a} h(x) = L$이면, $\lim_{x \to a} f(x) = L$이 성립한다.

이제 거듭제곱 함수 $f(x) = x^n$의 도함수를 구해보자. (풀이 생략) $$ f’(x) = n \cdot x^{n-1} $$

자연지수함수의 도함수 #

이전에 보았듯, 무리수 $e$는 극한과 무한대 개념을 사용해 다음과 같은 식으로 나타낼 수 있었다. $$e = \lim_{x \to \infty} (1 + \frac{1}{x})^x$$
- 여기서 $x$를 $\frac{1}{h}$로 바꾸면 다음과 같다. $\frac{1}{h}$가 한없이 커지면 $h$는 $0$에 수렴한다. $$e = \lim_{h \to 0} (1 + h)^{\frac{1}{h}}$$
- 이것을 정리하면 다음과 같은 수식을 얻을 수 있다. (풀이 생략) $$ \frac{\lim_{h \to 0}(e^h - 1)}{\lim_{h \to 0} h} = 1 $$
- 이것은 아래에서 도함수를 구할 때 요긴히 쓰인다.

이전에 봤던 도함수의 계산식은 다음과 같았다. $$ f’(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} $$
- 여기에 자연지수함수 $f(x) = e^x$를 대입하면 다음과 같이 자연지수함수의 도함수를 얻을 수 있다. (풀이 생략) $$ f’(x) = e^x $$
- 이것은 원함수와 동일하다.
- 함수를 미분했는데 결과가 동일하다면, 그 함수는 몇번을 미분해도 결과는 언제나 원함수와 동일할 것이다. 그래서 자연지수함수는 무한번 미분이 가능하다.

sin함수와 cos함수의 도함수 #

다음과 같은 극한식이 존재한다. (풀이 생략) $$ \lim_{h \to 0} \frac{\sin h}{h} = 1 $$ $$ \lim_{h \to 0} \frac{\cos h - 1}{h} = 1 $$
- 이것은 아래에서 도함수를 구할 때 요긴히 쓰인다.

$\sin$ 함수의 도함수
- 이전에 봤던 도함수 계산식에 $f(x) = \sin x$를 대입해서 구한다. (풀이 생략) $$ f’(x) = \cos x $$
$\cos$ 함수의 도함수
- 이전에 봤던 도함수 계산식에 $f(x) = \cos x$를 대입해서 구한다. (풀이 생략) $$ f’(x) = - \sin x $$

$\sin$ 함수를 여러번 미분하면 어떻게 될까? $$ f(x) = \sin x $$ $$ f’(x) = \cos x $$ $$ f’’(x) = - \sin x $$ $$ f’’’(x) = - \cos x $$ $$ f^{(4)}(x) = \sin x $$
- 네 번 미분했더니 원함수로 돌아왔다.
- 이것은 $\cos$함수도 마찬가지이다.
- 따라서 자연지수함수와 동일하게 $\sin$함수와 $\cos$함수도 무한번 미분이 가능한 함수이다.

급수 #

등비수열 #

수열(Sequence)
- 규칙에 따라 순서에 맞게 수를 나열한 것이다.
등비수열(Geometric sequence) $$ \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \frac{1}{32}, … $$
- 일정한 비(Ratio)로 증가하는 수열이다.
- 이때 사용되는 비를 공비(Common ratio) 라고 하며, 위 예제에서는 연속된 두 항이 $\frac{1}{2}$배씩 증가하므로 $\frac{1}{2}$가 공비이겠다.
- 첫번째 값을 초항(First term)이라고 하며 $a$로 표기한다. 공비는 $r$로, $n$번째 항은 $a_n$으로 표기한다. $$ a_n = a \cdot r^{n-1} $$

급수 #

급수(Series) $$\sum_{k=0}^n a_k = a_0 + a_1 + a_2 + a_3 + … + a_n$$
- 수열의 모든 값을 더한 것이다.
기하급수(Geometrix series) $$ \sum_{k=0}^{\infty} a \cdot r^k $$
- 등비수열의 급수를 기하급수라고 한다.
- 조건에 따라 무한대로 계속 증가하거나, 특정 수로 수렴하는 성질이 있다. 이것을 어떻게 파악할 수 있을까?

등비수열의 초항을 $a$, 공비를 $r$이라고 했을 때, $n$개의 유한한 등비급수를 $s_n$으로 표현하면 다음 식이 성립한다. $$ s_n = a + ar + ar^2 + ar^3 + … + ar^{n-1} $$

양변에 공비 $r$를 곱하면 다음과 같다. $$ r s_n = ar + ar^2 + ar^3 + … + ar^n $$
위 두식을 빼면 다음 식이 나온다. $$ s_n - rs_n = a - ar^n $$
이것을 정리하면 다음 식이 유도된다. $$ s_n = \frac{a(1 - r^n)}{1 - r} $$
기하급수는 무한 개의 요소를 가지므로, $n$에 극한을 설정하고 이를 전개하면 다음과 같다. $$ \lim_{n \to \infty} s_n = \lim_{n \to \infty} \frac{a(1 - r^n)}{1 - r} $$ $$ = \frac{a}{1-r} - \frac{a}{1-r} \cdot \lim_{n \to \infty} r^n $$

이 식을 바탕으로 해서 $r$의 값에 따라 기하급수 값이 발산하는지 수렴하는지 판단해볼 수 있다.

조건	의미
$r = 1 $	발산한다. $s_n = a + a + a + a + …$
$\|r\| \gt 1 $	발산한다. 공비 $r$을 곱할 수록 크기가 커지므로 $\lim_{n \to \infty} r^n$의 극한값이 발산한다.
$\|r\| \lt 1 $	수렴한다. 공비 $r$을 곱할 수록 크기가 작아지므로 극한값이 $0$으로 수렴한다.
$ r = -1 $	$\lim_{n \to \infty} r^n$의 값이 규칙적으로 $1$과 $-1$을 오고간다. 이러한 현상을 진동한다(Oscillate)고 표현하며, 발산으로 취급된다.

멱급수(Power series) $$ \sum_{n=0}^{\infty} a_n \cdot r^n = a_1 + a_2r + a_3r^2 + a_4r^3 + … $$
- 항마다 계수가 다른 급수이다.
비판정법(Ratio test)
- 멱급수가 수렴하는지 발산하는지 판단하기 위해서, 항비의 극한을 통해 판정하는 방법이다. $$ L = \lim_{n \to \infty} |\frac{a_{n+1}}{a_n}| $$
- $L$의 값은 다음과 같은 경우가 존재한다.
  
  조건 의미
  
  $L = 1$ 급수는 수렴할 수도, 발산할 수도 있다.
  
  $L \gt 1$ 급수는 발산한다.
  
  $L \lt 1$ 급수는 수렴한다.
- 멱급수가 수렴하기 위해 $r$이 가져야 할 범위를 수렴구간이라고 한다.
- 범위의 절반인 $1$의 값을 수렴반지름(Radius of convergence)이라고 한다.

조건	의미
$L = 1$	급수는 수렴할 수도, 발산할 수도 있다.
$L \gt 1$	급수는 발산한다.
$L \lt 1$	급수는 수렴한다.

앞의 기하 급수 예제를 멱급수의 관점에서 다시 살펴보자.
- 기하 급수는 모든 계수의 값이 동일한 멱급수라고 볼 수 있다. $$ \sum_{n=0}^{\infty} a \cdot r^n $$
- 이것을 비판정법에 적용하면 결괏값은 $n$과 무관하게 $|r|$이 나온다. $$ L = \lim_{n \to \infty} |\frac{a \cdot r^{n+1}}{a \cdot r^n}| = |r|$$
- 급수가 수렴하려면 $L \lt 1$ 조건을 만족해야 하는데, 이경우 $|r| \lt 1$ 와 같으므로 이전에 우리가 보았던 조건과 동일한 결과가 나왔음을 알 수 있다.

매클로린 급수 #

매클로린 급수(Maclaurin series) 또는 테일러 급수(Taylor series) $$ f(x) = a_1 + a_2x + a_3x^2 + a_4x^3 + a_5^4 + … $$ $$ f(x) = \frac{f(0)}{0!} + \frac{f’(0)}{1!}x + \frac{f’’(0)}{2!}x^2 + \frac{f’’’(0)}{3!}x^3 + … $$
- 무한정 미분이 가능한 함수를 $n$번 미분한 도함수에 $0$을 대입한 형태로 일반화 시켜서, 멱급수 형태로 나타낸 것이다.
- 매클로린 급수는 무한급수이므로, 무한 미분 가능한 함수만 이 수식을 만족하게 된다.

$$ a_n = \frac{f^{(n)}(0)}{n!} $$

자연지수함수 $ f(x) = e^x $를 매클로린 급수 형식으로 전개해보자. $$ f(x) = 1 + x + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + \frac{1}{4!}x^4 + … $$ $$ = \sum_{n = 0}^{\infty} \frac{x^n}{n!} $$
- 이 급수가 수렴하는지 알기 위해 비판정법을 진행해보면, $L$은 $0$이 된다. (풀이 생략)
- $L \lt 1$이므로 이 급수는 언제나 수렴하고, 자연지수함수의 매클로린 급수는 유효하다.

$\sin$함수 $ f(x) = \sin x $를 매클로린 급수 형식으로 전개해보자. $$ f(x) = 0 + x - 0 - \frac{1}{3!}x^3 + 0 + \frac{1}{5!}x^5 - 0 - \frac{1}{7!}x^7 + … $$ $$ = \sum_{n = 0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!} $$
- 이 급수가 수렴하는지 알기 위해 비판정법을 진행해보면, $L$은 $0$이 된다. (풀이 생략) 따라서 유효하다.

$\cos$함수 $ f(x) = \cos x $를 매클로린 급수 형식으로 전개해보자. $$ f(x) = 0 - x - \frac{1}{2!}x^2 + 0 + \frac{1}{4!}x^4 - 0 - \frac{1}{6!}x^6 + …$$ $$ = \sum_{n = 0}^{\infty} \frac{(-1)^n x^{2n}}{(2n)!} $$
- 이 급수가 수렴하는지 알기 위해 비판정법을 진행해보면, $L$은 $0$이 된다. (풀이 생략) 따라서 유효하다.

매클로린 급수는 컴퓨터에서 복잡한 근사값을 구할 때 유용하게 사용된다.
- 예를 들어서 $\sin$ 함수 값을 구해야 한다면?
- $x$에 급수 항을 추가함에 따라 $\sin x$의 값과 매우 가까워질 것이다.
- 따라서 각 급수항에 계승으로 나눈 상수를 미리 계산해두면 컴퓨터로 매우 빠르게 $\sin x$를 구할 수 있다.

오일러 공식 #

자연지수함수의 매클로린 급수 $$ e^x = 1 + x + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + \frac{1}{4!}x^4 + … $$
$\sin$함수의 매클로린 급수 $$ \sin x = 0 + x - 0 - \frac{1}{3!}x^3 + 0 + \frac{1}{5!}x^5 - 0 - \frac{1}{7!}x^7 + … $$
$\cos$함수의 매클로린 급수 $$ \cos x = 0 - x - \frac{1}{2!}x^2 + 0 + \frac{1}{4!}x^4 - 0 - \frac{1}{6!}x^6 + …$$

여기서 $\sin$ 함수와 $\cos$ 함수의 두 급수를 더해보자. $$ \cos x + \sin x = 1 + x - \frac{1}{2!}x^2 - \frac{1}{3!}x^3 + \frac{1}{4!}x^4 + \frac{1}{5!}x^5 - \frac{1}{6!}x^6 - \frac{1}{7!}x^7 + … $$
자연지수함수의 급수에 허수 단위 $i$를 넣어보자. $$ e^{ix} = 1 + ix - \frac{1}{2!}x^2 - \frac{i}{3!}x^3 + \frac{1}{4!}x^4 + \frac{i}{5!}x^5 - \frac{1}{6!}x^6 - \frac{i}{7!}x^7 + … $$
위 두 식의 차이는 짝수 항에 $i$가 붙어 있다는 것 뿐이다.
$ \cos x + \sin x$에서 짝수항은 $\sin$ 함수가 담당하므로, $\sin$함수에 $i$를 곱하면 두 식이 똑같아 진다. $$ e^{ix} = \cos x + i \sin x $$
여기에 $x$대신 각 $\theta$를 대입해 보면, 오일러 공식이 유도된다. $$ e^{i\theta} = \cos\theta + i \sin\theta $$

Chapter 14에서 $\cos\theta + i \sin\theta$는 복소평면에서 회전 변환을 담당하는 단위 복소수를 의미했다.
- 따라서 $e^{i\theta}$는 복소평면에서의 회전변환을 의미함을 알 수 있다.
이로써, 2차원 평면의 회전을 나타내는 방법이 하나 더 추가 되었다. 지금까지 행렬과 복소수를 사용해 표현했던 회전 변환은 오일러 공식을 사용해서 $e^{i\theta}$라는 자연지수함수로 더욱 간단하게 표현할 수 있게 되었다. $$ e^{i\theta} = (\cos\theta, \sin\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}$$
- 예를 들어, 각 $\alpha$, $\beta$의 회전변환은 오일러 공식에 의해 $e^{\alpha i}$, $e^{\beta i}$로 표현할 수 있다. 이 둘을 곱하면 $e^{(\alpha + \beta)i}$가 된다. 회전변환이 굉장히 단순화되었다.