[게임 수학] Chapter 14. 복소수: 2차원 평면의 수
Table of Contents
이득우의 게임 수학 책을 읽고 공부한 노트입니다.
복소수 #
- 체의 구조를 가지는 수 집합은 실수 외에도 복소수(Complex number) 가 있다.
- 복소수는 다음과 같이 실수(Real number) 와 허수(Imaginary number) 의 독립된 2개 요소로 구성된 수 집합이다.
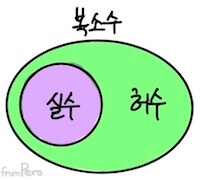
허수 #
- 허수 단위(Imaginary unit)
- $i$라는 기호를 사용한다.
- 제곱했을 때 $-1$이 되는 수를 말한다.
$$ i^2 = -1 $$
- 복소수는 실수부(Real part)와 허수부(Imaginary part)로 분리되어 있으며 허수부는 항상 $i$를 사용해서 표기한다.
- 그래서 실수부가 $a$, 허수부가 $b$인 복소수는 다음과 같이 표기한다.
$$ a + bi $$ $$ (a, b) $$
복소수의 구조 #
- 복소수 덧셈 연산의 성질
| 연산의 성질 | 수식 |
|---|---|
| 덧셈에 대해 닫혀 있음 | O |
| 덧셈에 대한 결합법칙이 성립함 | $$(a, b) + ((c, d) + (e, f)) = ((a, b) + (c, d)) + (e, f)$$ |
| 덧셈에 대한 교환법칙이 성립함 | $$(a, b) + (c, d) = (c, d) + (a, b)$$ |
| 덧셈에 대한 항등원의 존재함 | $$(a, b) + (0, 0) = (a, b)$$ |
| 덧셈에 대한 역원이 존재함 | $$(a, b) + (-a, -b) = (0, 0)$$ |
- 복소수 곱셈 연산의 성질
| 연산의 성질 | 수식 |
|---|---|
| 곱셈에 대해 닫혀 있음 | O |
| 곱셈에 대한 결합법칙이 성립함 | $$(a, b) \cdot ((c, d) \cdot (e, f)) = ((a, b) \cdot (c, d)) \cdot (e, f)$$ |
| 곱셈에 대한 교환법칙이 성립함 | $$(a, b) \cdot (c, d) = (c, d) \cdot (a, b)$$ |
| 덧셈과 곱셈에 대한 분배법칙이 성립함 | $$(a, b) \cdot ((c, d) + (e, f)) = (a, b) \cdot (c, d) + (a, b) \cdot (e, f)$$ |
| 곱셈에 대한 항등원의 존재함 | $$(a, b) \cdot (1, 0) = (a, b)$$ |
| 곱셈에 대한 역원이 존재함 | O (켤레 복소수 개념을 통해 알아보자…) |
- 복소수의 크기
- 2차원 벡터와 동일하게 실수부와 허수부를 제곱해 더한 다음, 제곱근을 취한다.
- 절댓값 기호를 써서 나타내며 복소수의 노름(Norm) 이라고도 부른다.
$$ |(a, b)| = |(a, -b)| = \sqrt{a^2 + b^2} $$
- 단위 복소수(Unit complex number)
- 크기가 1인 복소수이다.
- 켤레(Conjugate) 복소수
- 임의의 복소수를 $c$라고 하면 켤레 복소수는 $c^*$나 $\bar{c}$로 표시한다.
$$ c = a + bi = (a, b) $$ $$ c^* = a - bi = (a, -b) $$
- 켤레 복소수의 곱은 다음과 같은 성질이 있다.
$$ (c^*)^* = c $$ $$ c^*c = c^* $$ $$ (c_1c_2)^* = c_2^*c_1^* $$
- 어떤 복소수에 그 켤레 복소수를 곱하면 해당 복소수의 크기를 제곱한 값을 얻을 수 있다.
$$ cc^* = (a + bi) \cdot (a - bi) = a^2 + b^2 = |c|^2 $$
- 그러면 켤레 복소수를 이용해서 복소수의 역원을 구해보자.
- $c$의 역원인 $c^{-1}$에 켤레 복소수를 곱해보자.
$$ c^{-1} = \frac{1}{c} = \frac{c^*}{cc^*} $$ $$ (a + bi)^{-1} = \frac{1}{(a + bi)} = \frac{(a - bi)}{(a + bi)(a - bi)} = \frac{(a - bi)}{(a^2 + b^2)} $$
- 즉, $c$의 역원인 $c^{-1}$은 켤레 복소수에 복소수 크기에 관한 식으로 나타낼 수 있다.
$$ c^{-1} = \frac{c^*}{|c|^2} $$
- 단위 복소수의 역원은?
- 단위 복소수는 크기가 $1$이므로, 분모가 $1$이 된다. 따라서 곱셈 역원은 바로 켤레 복소수가 된다.
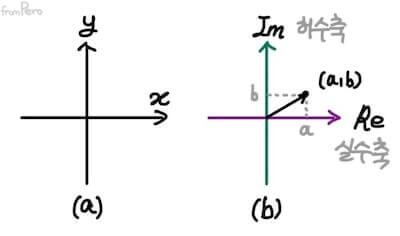
복소평면 #
- 복소평면(Complex plane)
- 아래 그림 (a)와 같이 2차원 실벡터 공간 $\mathbb{R}^2$의 벡터 $(a, b)$를 표현하기 위해서 서로 직교하는 $x$, $y$축을 사용한 것처럼,
- 복소수 역시 (b)와 같이 실수축과 허수축을 직각으로 교차시키는 방식으로 표현할 수 있다.
- 이것을 복소평면이라고 한다.
- 여기에 복소수 $(a, b)$를 평면 상에 다음과 같이 표현할 수 있겠다.
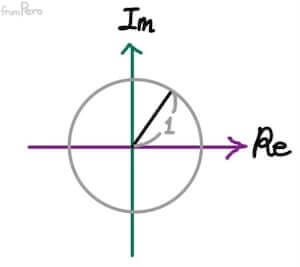
- 크기가 $1$인 단위 복소수를 모아 복소평면에서 표현하면 단위원이 만들어진다.
단위 복소수와의 곱 #
- 허수부가 $0$인 임의의 복소수 $(a, 0)$에 $i$라는 단위 복소수를 곱해보자.
$$ (a + 0i) \cdot (0 + i) = (0 + ai) = (0, a) $$
- 이것을 평면 상에 나타내보면, $(0, a)$는 복소수 $(a, 0)$를 $90^{\circ}$ 회전시킨 결과다.
- 이 결과에 또 다시 단위 복소수 $(0, i)$를 곱하면 계속 $90^{\circ}$씩 회전한다.
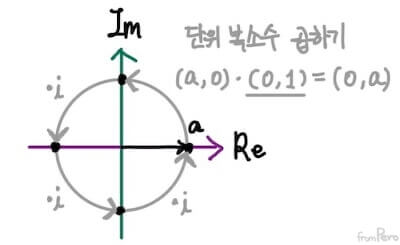
- 따라서 임의의 복소수 $(a, b)$에 단위 복소수 $i$를 곱한 결과는 해당 복소수를 $90^{\circ}$ 회전시킨 결과와 같다.
$$ (a, b) \cdot (0, 1) = (-b, a) $$
- 이것은 Chapter 5에서 보았던 좌표 평면에서의 $90^{\circ}$ 회전과 동일하다.
- 삼각함수 공식 $\cos^2\theta + \sin^2\theta = 1$를 이용해서 단위 복소수를 다음과 같이 표현할 수 있겠다. (참고로, 삼각함수를 사용하는 경우에는 허수의 $i$가 앞에 오는게 일반적이다.)
$$ \cos\theta + i\sin\theta = (\cos\theta, \sin\theta) $$
- 이렇게 삼각함수로 나타낸 단위 복소수에다가 임의의 복소수 $(x, y)$를 곱하면?
$$ (\cos\theta, \sin\theta) \cdot (x, y) = (x\cos\theta - y\sin\theta, y\cos\theta + x\sin\theta) $$
- 이것은 Chapter 5에서 다룬 2차원 공간의 회전행렬 R에 2차원 벡터 $(x, y)$를 곱한 결과와 같다.
$$ R = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} $$ $$ \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x\cos\theta - y\sin\theta \\ y\cos\theta + x\sin\theta \end{bmatrix} $$
- 따라서, 임의의 복소수에 단위 복소수를 곱하는 것은 복소평면에서의 회전변환을 의미한다.

- 이번에는 서로 다른 각을 갖는 2개의 복소수를 곱한 결과를 보자.
$$ (\cos\alpha, \sin\alpha) \cdot (\cos\beta, \sin\beta) = (\cos\alpha\cos\beta - \sin\alpha\sin\beta, \sin\alpha\cos\beta + \sin\beta\cos\alpha) $$
- Chapter 5에서 살펴본 삼각함수의 덧셈 정리를 사용하면 다음과 같이 정리할 수 있다.
$$ (\cos(\alpha + \beta), sin(\alpha + \beta)) $$
- 따라서, 서로 다른 두 각을 회전 변환한 후 곱셈 연산을 하는 것은 두 각의 합을 회전 변환하는 것과 동일하다는 것을 알 수 있다.
- 이번에는 복소수 곱셈의 항등원인 $(1, 0)$의 의미를 생각해보자.
- 이것은 실수에서 곱셈의 항등원인 $1$과 동일하다. 복소수 $1$은 단위 복소수이다.
- 삼각함수로 표현하면 다음과 같이 각 $0^{\circ}$에 대응하는 수다.
$$ (1, 0) = (\cos0^{\circ}, \sin0^{\circ}) $$
- 따라서, 곱셈의 항등원을 곱한다는 것은 아무런 변화가 일어나지 않는 $0^{\circ}$의 회전 변환이라고 해석할 수 있다.
켤레 복소수의 회전 변환 #
- 복소평면에서 켤레 복소수를 시각화해보자.
- 임의의 복소수 $(a, b)$의 켤레 복소수 $(a, -b)$는 다음과 같다.
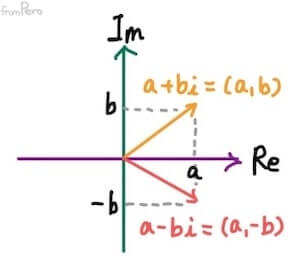
- 이것은 실수부 축($Re$)을 중심으로 서로 대칭된 형태이다.
- 이번에는 단위 복소수의 켤레 복소수를 생각해보자.
- 단위 복소수 $(\cos\theta, \sin\theta)$의 켤레 복소수는 $(\cos\theta, -\sin\theta)$이다.
- 여기에 삼각함수의 성질을 활용하면 켤레 복소수를 다음과 같이 나타낼 수 있다.
$$ (\cos\theta, -\sin\theta) = (\cos(-\theta), \sin(-\theta)) $$
- 즉, 단위 복소수가 실수 축에 위치한 $(1, 0)$을 각 $\theta$만큼 회전한 수를 의미한다면, 켤레 복소수는 반대 방향인 $-\theta$만큼 회전한 수를 의미한다.
- 따라서, 임의의 복소수 $(a, b)$에 단위 복소수를 곱하면 반시계 방향으로 회전이 발생하는데, 단위 복소수의 켤레 복소수를 곱하면 시계 방향의 회전이 발생한다.

- 단위 복소수와 켤레 복소수를 곱한 값은 복소수 크기의 제곱이므로 $1$이 된다.
- 아래 식을 변환의 관점에서 보면 각 $\theta$만큼 회전한 후 바로 $-\theta$만큼 거꾸로 회전하는 변환을 의미한다.
- 이 결과는 아무런 변화 없는 $0^{\circ}$ 회전 변환을 의미하므로 복소수 곱셈의 항등원 $(1, 0)$이 됨을 다시 한 번 확인할 수 있다.
$$ c \cdot c^* = a^2 + b^2 = \sin^2\theta + \cos^2\theta = 1 $$
복소수와 행렬의 관계 #
- 복소수를 수의 관점이 아닌 변환에 관점에서 보자.
- 2차원 복소평면 상의 복소수를 2차원 행렬에 대응할 수 있다.
- 단위 복소수가 2차원의 회전 변환행렬과 같다고 해보자.
$$ \cos\theta + i\sin\theta = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} $$
- 회전 변환행렬을 분리해 정리하면 다음과 같다.
$$ \cos\theta + i\sin\theta = \cos\theta \cdot \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} + \sin\theta \cdot \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$$
- 실수부에 대응하는 행렬을 $I$로 하고, 허수에 대응하는 행렬을 $J$라고 하자.
$$ I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} $$ $$ J = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} $$
- 실수부 행렬 $I$는 항등행렬이지만, 허수부 행렬 $J$는 $90^{\circ}$ 회전 변환행렬이다.
- $J$를 두 번 곱하면 $-I$가 나오며 이것은 $-1$에 대응한다.
$$ J \cdot J = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} = -I $$
- 이는 두 번 곱하면 $-1$이 나오는 허수 단위의 성질과도 일치한다.
$$ i \cdot i = -1 $$