[Game Math] Chapter 13. 절두체: 최적화된 3차원 공간 (1)

절두체 컬링 #

• 절두체 컬링(Frustum culling)
  • 절두체를 구성하는 6개의 평면에 대해 각각 평면의 방정식을 세우고, 그것을 활용해서 게임 오브젝트가 평면의 바깥에 있는지 확인한다.
  • 바깥에 있다면, 그리지 않는다.

평면의 방정식 #

• 절두체를 구성하는 평면의 방정식을 알아보자.
  • Chapter 8에서 살펴본 것처럼, 주어진 세 점으로 두 벡터를 생성해서 평면 상의 모든 점을 생성할 수 있다.
  • 하지만 3차원 공간의 평면은 앞면과 뒷면이 존재하기 때문에 이를 구분할 수 있어야 하겠다.
  • 따라서 평면이 바라보는 방향을 알려주는 법선 벡터와 평면 상에 위치한 한 점을 제공하는 방법을 사용한다. 이 때 법선 벡터는 크기를 1로 정규화한다.
    

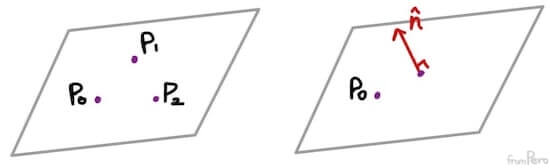
• 법선벡터와 평면 위의 두 점을 지나는 벡터는 서로 직교하기 때문에 두 벡터의 내적은 $0$이 된다.
  • 따라서 법선벡터 $\hat{n} = (a, b, c)$와 점 $P_0 = (x_0, y_0, z_0)$에서 $P = (x, y, z)$로 향하는 벡터를 내적하면 다음과 같다.

$$ \hat{n} \cdot (P - P_0) = (a, b, c) \cdot (x - x_0, y - y_0, z - z_0) = 0 $$ $$ = ax + by + cz - (ax_0 + by_0 + cz_0) = 0 $$

• 여기서 법선벡터 $\hat{n} = (a, b, c)$와 점 $P_0 = (x_0, y_0, z_0)$은 사전에 주어진 값이므로 $- (ax_0 + by_0 + cz_0)$는 미리 계산할 수 있는 상수 값이다. 이것을 간단히 $d$로 치환하면 다음과 같다.
• 평면의 방정식(The equation of plane) $$ ax + by + cz + d = 0 $$

• 여기서 $d$의 의미를 찾아보자.

$$d = -(ax_0 + by_0 + cz_0)$$ $$ d = -\hat{n} \cdot (x_0, y_0, z_0)$$ $$ d = -\hat{n} \cdot \vec{OP_0} = -\hat{n} \cdot \vec{p}$$

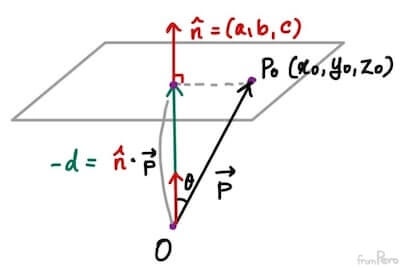
• 그렇다면 $\hat{n} \cdot \vec{p}$는 무엇을 의미할까?
• Chapter 7에서 배운 벡터 내적의 $\cos$공식을 떠올려보자.

$$\hat{n} \cdot \vec{p} = | \hat{n} | | \vec{p} | \cos\theta$$

• 법선 벡터의 크기는 $1$이므로 다음과 같이 정리된다.

$$\hat{n} \cdot \vec{p} = | \vec{p} | \cos\theta$$

• 따라서 $\hat{n} \cdot \vec{p}$이란 $\vec{p}$벡터를 법선 벡터 $\hat{n}$에 투영한 벡터의 크기를 의미한다.
  • 즉, 원점에서 평면까지의 최단 거리인 것이다.
• $d$의 값은 마이너스를 붙인 $-\hat{n} \cdot \vec{p}$이므로 원점으로부터 평면의 최단 거리에 음의 부호를 설정한다.
  • 그래서 $d$는 최단 거리와 방향이라는 두 가지 정보를 담고 있다.

• $d$의 부호
  • $d$의 값이 양수이다.
    • 평면이 바라보는 방향은 원점을 향한다.
    • 즉, 원점은 평면의 바깥에 있다.
  • $d$의 값이 음수이다.
    • 평면이 바라보는 방향은 원점에서 멀어지는 방향을 가진다.
    • 즉, 원점은 평면의 안쪽에 있다.
• $d$의 절댓값
  • 평면에서 원점까지의 최단 거리.
• $d$의 값이 $0$ 이다.
  • 평면이 원점을 품었다.

• 주어진 점이 평면의 안쪽에 있는지 바깥쪽에 있는지 판별하기.
  • $d$값의 성질을 응용해보자.
    

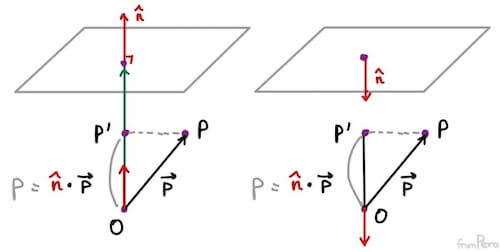
• 위 그림과 같이 벡터 $\vec{p}$를 법선 벡터에 내적한 값을 $p$라고 하자.
  • $p$가 양수면? 벡터 $\vec{p}$는 법선 벡터와 같은 방향을 향한다.
  • $p$가 음수면? 벡터 $\vec{p}$는 법선 벡터와 반대 방향을 향한다.
  • 위 그림에서는 $p$가 양수이겠다.
• 그렇다면 $p$와 $d$를 더한 값은 어떨까?
  • $p + d$가 음수면? 점 $P$는 평면의 안쪽에 있다.
  • $p + d$가 양수면? 점 $P$는 평면의 바깥쪽에 있다.
• 따라서 법선 벡터 $(a, b, c)$와 $d$를 사용해 주어진 점 $P = (x_1, y_1, z_1)$이 평면의 바깥쪽에 있는지 판단하는 수식은 다음과 같다.
  • $(a, b, c) \cdot (x_1, y_1, z_1) + d > 0 $
• 그리고 평면에서 해당 점까지의 최단 거리는 다음과 같다.
  • $distance = |(a, b, c) \cdot (x_1, y_1, z_1) + d | $

평면의 방정식의 정규화 #

• 크기가 $1$이 아닌 주어진 법선 벡터를 구성하는 세 계수 $(a, b, c)$를 정규화해서 $(a’, b’, c’)$를 만들어 보자.
  • 이것은 법선 벡터의 크기로 나누면 구할 수 있다.

$$ (a’, b’, c’) = \frac{(a, b, c)}{\sqrt{a^2 + b^2 + c^2}} $$

• $d$를 정규화한 $d’$를 만들어 보자.

$$ d = -\hat{n} \cdot \vec{p} = - |\hat{n}||\vec{p}|\cos\theta $$ $$ d’ = -|\vec{p}|\cos\theta $$

• 따라서 다음과 같은 관계가 나온다.

$$ d’ = \frac{d}{|\vec{n}|} $$

• 즉, $d$의 경우에도 동일하게 법선 벡터의 크기로 나누면 되는 것이다.

$$ \frac{ax + by + cz + d}{\sqrt{a^2 + b^2 + c^2}} = 0 $$

• 2차원 직선의 방정식에서의 최단 거리
  • 임의의 한 점 $(x_1, y_1)$에서 임의의 직선 $ax + by + c = 0$ 까지의 최단 거리는 어떻게 구할 수 있을까?
    

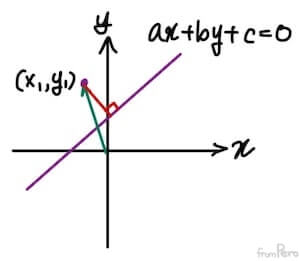
• 평면의 방정식을 정규화한 값과 내적을 활용해 구할 수 있겠다.

$$ \frac{ | ax_1 + by_1 + c | }{ \sqrt{a^2 + b^2 } } $$

평면의 방정식을 활용한 절두체 표현 #

• 절두체 상단 평면을 무한하게 확장하면, 그 평면은 원점을 품게 된다.
  • 이것은 근평면, 원평면을 제외한 나머지 평면에 대해서도 동일하다.
  • 따라서 근평면, 원평면을 제외한 나머지 평면을 구성하는 평면의 방정식 $d$값은 $0$이겠다.
• 상단 평면의 경우 아래 그림과 같이 구할 수 있으므로, 같은 방식으로 네 평면의 방정식을 구할 수 있다.

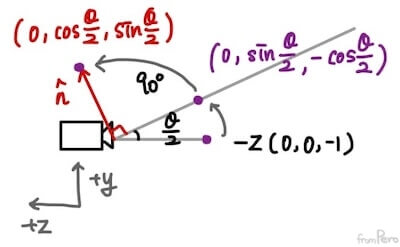
• 절두체 상단 평면의 방정식

$$ \cos\frac{\theta}{2}y + \sin\theta\frac{\theta}{2}z = 0 $$

• 절두체 하단 평면의 방정식

$$ -\cos\frac{\theta}{2}y + \sin\theta\frac{\theta}{2}z = 0 $$

• 절두체 좌측 평면의 방정식

$$ \cos\frac{\theta}{2}x + \sin\theta\frac{\theta}{2}z = 0 $$

• 절두체 우측 평면의 방정식

$$ -\cos\frac{\theta}{2}x + \sin\theta\frac{\theta}{2}z = 0 $$

• 근평면의 경우, 원점으로부터의 거리는 $n$이므로, 평면의 방정식의 $d$의 값은 $n$이 된다. 그리고 법선 벡터의 값은 $(0, 0, 1)$이 된다.

$$(0, 0, 1) \cdot (x, y, z) - (0, 0, 1) \cdot (0, 0, -n) = 0 $$ $$ \therefore z + n = 0 $$

• 원평면의 경우에는 거리가 $f$가 되며, 법선 벡터의 값은 $(0, 0, -1)$이 된다.

$$(0, 0, -1) \cdot (x, y, z) - (0, 0, 1) \cdot (0, 0, f) = 0 $$ $$ \therefore -z -f = 0 $$

• 이 때, 함부로 수식을 옮기면 안 된다. 만약 $0 = z + f$와 같이 옮긴다면, 평면의 방향은 원평면의 반대 방향인 원점을 향한다. 따라서 $-z -f = 0 $와 $0 = z + f$는 서로 다른 평면이다.

원근 투영 행렬로부터 평면의 방정식 만들기 #

• 원근 투영 행렬을 사용해서 절두체 컬링을 좀 더 간편하게 구현할 수 있다.
• 뷰 공간의 점이 NDC좌표까지 변환됐을 때, NDC좌표를 구성하는 $x$, $y$, $z$ 세 축의 값이 $[-1, 1]$ 범위에 있다면 해당 점은 절두체 영역 안 쪽에 있다는 것을 의미한다.

$$ -1 \leq n_x \leq 1 $$ $$ -1 \leq n_y \leq 1 $$ $$ -1 \leq n_z \leq 1 $$

• 이 때 NDC좌표는 클립 좌표의 마지막 차원 $w$로 나눈 결과값이므로 다음과 같다.

$$ -1 \leq \frac{x}{w} \leq 1 $$ $$ -1 \leq \frac{y}{w} \leq 1 $$ $$ -1 \leq \frac{z}{w} \leq 1 $$ $$ -w \leq x \leq w $$ $$ -w \leq y \leq w $$ $$ -w \leq z \leq w $$

• 여기서 $x$, $y$, $z$란?

$$ P \cdot \vec{v} = \begin{bmatrix} \frac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0 & 0 & \frac{n + f}{n - f} & \frac{2nf}{n - f} \\ 0 & 0 & -1 & 0 \end{bmatrix} \begin{bmatrix} v_x \\ v_y \\ v_z \\ 1 \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} $$

• 이것은 원근 투영 행렬의 4개의 행벡터와 $\vec{v}$의 내적으로 바꿔 쓸 수 있다.

$$ \begin{bmatrix} P_{row1} \cdot \vec{v} \\ P_{row2} \cdot \vec{v} \\ P_{row3} \cdot \vec{v} \\ P_{row4} \cdot \vec{v} \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} $$

• 이것을 부등식에 치환하면 다음과 같다.

$$ -P_{row4} \cdot \vec{v} \leq P_{row1} \cdot \vec{v} \leq P_{row4} \cdot \vec{v} $$ $$ -P_{row4} \cdot \vec{v} \leq P_{row2} \cdot \vec{v} \leq P_{row4} \cdot \vec{v} $$ $$ -P_{row4} \cdot \vec{v} \leq P_{row3} \cdot \vec{v} \leq P_{row4} \cdot \vec{v} $$

• 이것을 분리해 6개의 부등식으로 표현할 수 있겠다.

$$ (P_{row4} + P_{row1} \cdot \vec{v}) \geq 0 $$ $$ (P_{row4} - P_{row1} \cdot \vec{v}) \geq 0 $$ $$ (P_{row4} + P_{row2} \cdot \vec{v}) \geq 0 $$ $$ (P_{row4} - P_{row2} \cdot \vec{v}) \geq 0 $$ $$ (P_{row4} + P_{row3} \cdot \vec{v}) \geq 0 $$ $$ (P_{row4} - P_{row3} \cdot \vec{v}) \geq 0 $$

• 이 부등식이 모두 참이면 점 $\vec{v}$는 절두체 영역 내부에 있음을 의미한다.
• 여기서 행벡터가 $P_{rown} = (a, b, c, d)$라고 하고, 뷰 공간의 점이 $\vec{v} = (x, y, z, 1)$라고 할 때 내적의 결과는 다음과 같다.

$$ ax + by + cz + d \geq 0 $$

• 하지만 법선벡터 $(a, b, c)$의 크기가 $1$이 아니므로, 정규화 해야 한다.

$$ \frac{ ax + by + cz + d }{ \sqrt{ a^2 + b^2 + c^2 } } = 0 $$

• 위 결과는 모두 절두체 내부를 향할 것이다. 따라서 외부에 있는지를 검출하기 위해서는 부호를 반전시켜 주어야 한다.

$$ - ( \frac{ ax + by + cz + d }{ \sqrt{ a^2 + b^2 + c^2 } } ) > 0 $$

• 원근 투영 행렬을 사용해서 절두체 컬링하는 예제이다.

struct Plane
{
public:
    FORCEINLINE constexpr float Distance(const Vector3& InPoint) const;
    FORCEINLINE constexpr bool IsOutside(const Vector3& InPoint) const;
    
    Vector3 Normal = Vector3::UnitY;  // (a, b, c)
    float D = 0.f;  // 상수 d의 값
};

Plane::Plane(const Vector4& InVector4)
{
    Normal = InVector4.ToVector3();  // (a, b, c)
    D = InVector4.W;  // 상수 d의 값
    Normalize();
}

// 정규화 한다. 
void Plane::Normalize()
{
    // a^2 + b^2 + c^2
    float squaredSize = Normal.SizeSquared();
    
    // 크기가 1이면 정규화할 필요 없다. 
    if (Math::EqualsInTolerance(squaredSize, 1.f))
    {
        return;
    }
    
    // 1 / sqrt(a^2 + b^2 + c^2)을 고속 역제곱근(Fast inverse square root) 함수로 구한다. 
    float invLength = Math::InvSqrt(squaredSize);
    
    // 곱해서 정규화한다. 
    Normal *= invLength;
    D *= invLength;
}


// p + d를 리턴한다. 
FORCEINLINE constexpr float Plane::Distance(const Vector3& InPoint) const
{
    return Normal.Dot(InPoint) + D;
}

// Distance의 반환값이 양수이면 그 점은 평면의 바깥에 있다. 
FORCEINLINE constexpr bool Plane::IsOutside(const Vector3& InPoint) const
{
    return Distance(InPoint) > 0.f;
}

FORCEINLINE constexpr BoundCheckResult Frustum::CheckBound(const Vector3& InPoint) const
{
    // 6개의 평면에 대해 테스트를 진행한다. 
    for (const auto& p : Planes) 
    {
        // 한 평면이라도 밖에 있으면 점은 외부에 있음으로 판별하고 함수를 종료한다. 
        if (p.IsOutside(InPoint)) 
        {
            return BoundCheckResult::Outside;
        }
        // 오차 범위 내의 거리가 0에 근접하면 겹치는 것으로 판별하고 종료한다. 
        else if (Math::EqualsInTolerance(p.Distance(InPoint), 0.f))
        {
            return BoundCheckResult::Intersect;
        }
    }

    // 모든 평면에 대해 위 테스트를 통과하면 안쪽으로 판별한다. 
    return BoundCheckResult::Inside;
}

// 렌더링 로직을 담당하는 함수
void SoftRenderer::Render3D()
{
    // 렌더링 로직에서 사용하는 모듈 내 주요 레퍼런스
    const GameEngine& g = Get3DGameEngine();
    auto& r = GetRenderer();
    const CameraObject& mainCamera = g.GetMainCamera();

    // 배경에 기즈모 그리기
    DrawGizmo3D();

    // 렌더링 로직의 로컬 변수
    const Matrix4x4 vMatrix = mainCamera.GetViewMatrix();
    const Matrix4x4 pMatrix = mainCamera.GetPerspectiveMatrix();  // 원근 투영 행렬을 가져온다. 
    const Matrix4x4 pvMatrix = mainCamera.GetPerspectiveViewMatrix();

    // 절두체 구축을 위한 투영 행렬의 설정
    Matrix4x4 ptMatrix = pMatrix.Transpose();

    // 절두체를 구성하는 평면의 방정식
    // 절두체를 구성하는 6개의 평면을 생성한다. 
    std::array<Plane, 6> frustumPlanes = {
        Plane(-(ptMatrix[3] - ptMatrix[1])), // +Y
        Plane(-(ptMatrix[3] + ptMatrix[1])), // -Y
        Plane(-(ptMatrix[3] - ptMatrix[0])), // +X
        Plane(-(ptMatrix[3] + ptMatrix[0])), // -X
        Plane(-(ptMatrix[3] - ptMatrix[2])), // +Z
        Plane(-(ptMatrix[3] + ptMatrix[2])), // -Z
    };

    // 절두체 선언 
    Frustum frustumFromMatrix(frustumPlanes); // 평면의 배열을 인자로 넣어 절두체를 구축한다. 

    // 절두체 컬링 테스트를 위한 통계 변수 
    size_t totalObjects = g.GetScene().size(); // 씬에 속한 전체 게임 오브젝트 수를 파악한다. 
    size_t culledObjects = 0; // 렌더링이 진행된 게임 오브젝트 수를 파악한다. 
    size_t renderedObjects = 0; // 렌더링이 진행된 게임 오브젝트 수를 파악한다. 

    for (auto it = g.SceneBegin(); it != g.SceneEnd(); ++it)
    {
        const GameObject& gameObject = *(*it);
        if (!gameObject.HasMesh() || !gameObject.IsVisible())
        {
            continue;
        }

        // 렌더링에 필요한 게임 오브젝트의 주요 레퍼런스를 얻기
        const Mesh& mesh = g.GetMesh(gameObject.GetMeshKey());
        const TransformComponent& transform = gameObject.GetTransform();

        // 절두체 컬링 구현
        // 게임 오브젝트의 위치를 뷰 공간으로 변환한다. 
        Vector4 viewPos = vMatrix * Vector4(transform.GetPosition());
        
        // 뷰 공간의 위치가 절두체 영역의 외부에 있는지 검사한다. 
        if (frustumFromMatrix.CheckBound(viewPos.ToVector3()) == BoundCheckResult::Outside)
        {
            // 그리지 않고 건너뜀
            culledObjects++;
            continue;
        }

        // 최종 행렬 계산
        Matrix4x4 finalMatrix = pvMatrix * transform.GetModelingMatrix();

        // 메시 그리기
        DrawMesh3D(mesh, finalMatrix, gameObject.GetColor());

        // 그린 물체를 통계에 포함
        renderedObjects++;
    }

    r.PushStatisticText("Total GameObjects : " + std::to_string(totalObjects));
    r.PushStatisticText("Culled GameObjects : " + std::to_string(culledObjects));
    r.PushStatisticText("Rendered GameObjects : " + std::to_string(renderedObjects));
}