[게임 수학] Chapter 12. 원근 투영: 화면에 현실감을 부여하는 변환
Table of Contents
이득우의 게임 수학 책을 읽고 공부한 노트입니다.
원근 투영 변환의 원리 #
- 투시 원근법(Perspective projection drawing)
- 시선을 한 점에 고정시키고, 고정된 점으로부터 화폭까지 곧게 뻗은 실을 활용해서 그림을 그려나가는 것이다.
- 원근 투영 변환(Perspective projection transformation)
- 투시 원근법의 원리를 적용하기 위해서 공간의 모든 점이 한 점을 향해 모이는 형태로 변환하는 것이다.
- 즉, $x$, $y$, $z$축이 모두 직교하는 정육면체 형태를 가진 뷰 공간을, 카메라의 한 점으로 모이는 사각뿔 형태를 가진 공간으로 변환하는 작업이다.
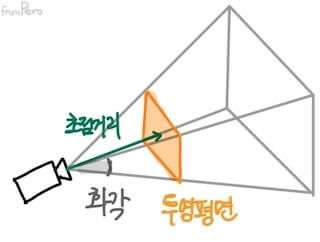
- 화각(Field of view)
- 카메라를 통해서 이미지를 담을 수 있는 각을 말한다.
- 카메라에 화각을 설정하면 좌우와 위아래가 균등한 사각뿔 영역이 만들어진다.
- 투영 평면(Projection plane)
- 3차원 공간을 원근 투영 변환한 후에는 그것을 2차원의 모니터 평면에 담아내야 한다. 이를 위해서 모든 물체의 상이 맺히는 가상의 평면을 생성해야 하는데 이것을 투영 평면이라고 한다.
- 초점 거리(Focal length)
- 카메라로부터 투영 평면까지의 거리이다.
- NDC(Normalized device coordinate)
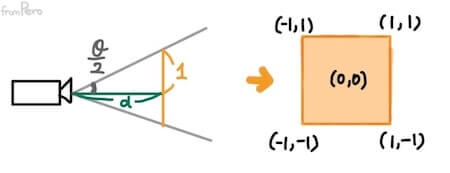
- 원근 투영 변환을 위해서는 먼저 투영 평면의 위치를 지정해야 한다. 일반적으로 투영 평면의 위치는 계산의 편의를 위해서 위 아래의 크기가 각각 $1$이 되는 지점으로 결정한다. 따라서 좌우와 상하가 $[-1, 1]$의 범위를 가지는 정사각형의 모습을 띤다.
- 이 정사각형 영역은 2차원 평면의 좌표 시스템을 가지는데 이를 NDC라고 한다.
- NDC는 가운데 중점을 원점으로 설정한다.
- NDC가 언제나 일정한 값을 가진다면, 화각에 따라 초점 거리가 달라질 수밖에 없다.
- 화각이 커질 수록 초점 거리는 가까워지고, 화각이 작아질 수록 초점 거리는 멀어지겠다.
$$\tan(\frac{\theta}{2}) = \frac{1}{d}$$ $$ d = \frac{1}{\tan(\frac{\theta}{2})}$$
- 사영 공간(Projective space)
- 지금까지의 공간 변환은 $x$, $y$, $z$축이 모두 직교하고 정육면체 형태의 3차원 공간이었다. 하지만 원근 투영 변환을 거치면 사각뿔 형태로 바뀌게 된다. 이것을 사영 공간이라고 한다.
- $x$, $y$축은 여전히 직교하므로 유클리드 공간과 동일한 성질을 가진다.
- 하지만 $z$축은 독립적으로 행동하지 않고 $x$, $y$축에 모두 영향을 준다. 이것이 초점 거리에 따라 투영 평면의 면적이 달라지는 이유이기도 하겠다.
- 그렇다면 원근 투영 변환에 대응하는 행렬은 어떻게 설계할 수 있을까?
- $x$축을 배제하고 $y$, $z$축으로 공간을 설정하고 투영 평면에 상이 맺히는 과정을 생각해보자.
- 뷰공간의 점 $P_{view}$가 투영 평면에 투영된 점을 $P_{ndc}$라고 한다면 좌표는 다음과 같다.
$$P_{view} = (0, v_y, v_z)$$ $$P_{ndc} = (0, n_y)$$
- 두 점의 관계를 닮은꼴 삼각형 두개로 알아보면 다음과 같은 비가 성립된다.
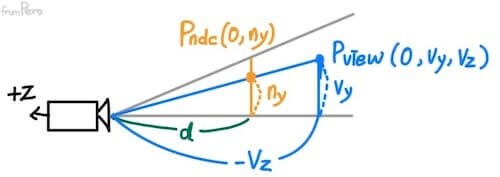
$$n_y : d = v_y : -v_z$$ $$n_y = \frac{d \cdot v_y}{-v_z}$$
- 카메라의 좌우 상하 시야각은 동일하므로 NDC의 $x$값 또한 $y$값을 $0$으로 고정한 후 $x$, $z$축의 평면을 사용하는 방식으로 구할 수 있겠다.
- 따라서 초점 거리와 뷰 좌표로부터 $P_{ndc}$를 구할 수 있다.
$$P_{ndc} = (n_x, n_y) = (\frac{d \cdot v_x}{-v_z}, \frac{d \cdot v_y}{-v_z}) = -\frac{d}{v_z}(v_x, v_y)$$
- 이제 NDC좌표를 계산했으니, 이 좌표를 모니터 해상도 만큼 가로 세로로 늘려주면 최종 스크린 좌표가 완성된다.
- 근데 가로 세로 해상도가 다르기 때문에 늘리면 물체가 찌그러지겠다.
- 가로 세로의 비를 종횡비(Aspect ratio) 라고 한다. 종횡비를 파악해서 미리 NDC영역에서 찌그러트린 다음에 펼치면 문제 해결이 가능하겠다.
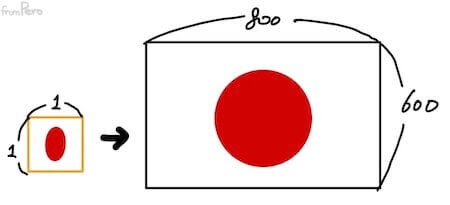
- 예를 들어, $800 \times 600$해상도에서 세로 크기를 기준으로 잡은 종횡비는 $1.3333$이다. 이 종횡비를 $a$라고 하자.
- 그러면 좌우로 찌그러트리기 위해서 $x$축에 종횡비의 역수 $\frac{1}{a}$를 곱하면 되겠다.
$$P_{ndc} = -\frac{d}{v_z}(\frac{v_x}{a}, v_y)$$
-
이렇게 최종 NDC값을 계산하는 원근 투영 행렬 $P$를 다음과 같이 설계할 수 있겠다. $$P_{ndc} = P \cdot \vec{v} = \begin{bmatrix} \frac{1}{a} \cdot \frac{d}{-v_z} & 0 \\ 0 & \frac{d}{-v_z} \end{bmatrix} \begin{bmatrix} v_x \\ v_y \end{bmatrix}$$
- 하지만 한 가지 아쉽다. 변환할 점의 $z$값이 행렬에 사용되다보니 변환할 점마다 항상 행렬을 새롭게 생성해야 한다.
- Chapter 5에서 본것처럼 미리 곱해둔 행렬을 계속 사용한다면 굉장히 연산량을 줄일 수 있겠다.
-
이건 어떨까? $-\vec{v_z}$값을 행렬에서 제거하고 대신 행렬의 결괏값에서 $-\vec{v_z}$를 나누어 주는 거다.
$$P_{ndc} = P \cdot \vec{v} = \begin{bmatrix} \frac{d}{a} & 0 & 0 \\ 0 & d & 0 \\ 0 & 0 & -1 \end{bmatrix} \begin{bmatrix} v_x \\ v_y \\ v_z \end{bmatrix} = \begin{bmatrix} \frac{d}{a} \cdot v_x \\ d \cdot v_y \\ -v_z\end{bmatrix}$$
- 클립 좌표(Clip coordinate)
- 이렇게 원근 투영 행렬 $P$로 변환되는 좌표계를 클립 좌표라고 부르며 다음과 같이 계산한다.
$$P_{clip} = (\frac{d}{a} \cdot v_x , d \cdot v_y , -v_z)$$
- 이 클립좌표를 세 번째 값인 $-v_z$로 나누면 NDC좌표를 얻을 수 있다.
$$P_{ndc} = (\frac{d \cdot v_x}{-v_z \cdot a}, \frac{d \cdot v_y}{-v_z}, 1)$$
동차 좌표계 #
- 동차 좌표계(Homogenous coordinate system)
- 한 차원 높인 벡터를 사용하는 것을 동차 좌표계라고 한다.
- 동차란? 모든 항의 차수가 같음을 의미한다.
- 사영 공간이 사용하는 좌표계는 동차 좌표계이다. 왜냐하면…
- 3차원의 사영 공간에서 평행하게 점을 이동시키면?
- 카메라에 멀어질 수록 투영된 좌푯값이 투영 평면의 원점에 가까워지고, 카메라에 가까워질수록 멀어진다.
- 즉, 사영 공간의 점과 투영된 점의 좌표는 반비례 관계이다.
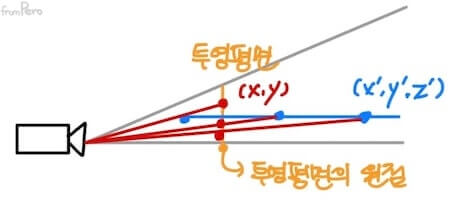
- 사영 공간의 점을 $(x’, y’, z’)$라고 하고, 해당 점이 투영된 NDC좌표를 $(x, y)$라고 하자. 그러면 NDC 좌푯값은 마지막 차원값 $z’$에 반비례로 영향을 받으므로 다음과 같은 관계가 성립한다.
$$x = \frac{x’}{z’}$$ $$y = \frac{y’}{z’}$$
- 사영 공간의 좌표로 직선의 방정식을 표현해보자. 위의 $x$, $y$를 직선의 방정식 $y = ax + b$에 대입해보자.
- 아래와 같이 세 미지수의 차수가 모두 1차식으로 동일한 방정식이 만들어진다. 이렇게 미지수에 대한 차수가 동일한 방정식을 동차 방정식이라고 한다.
- 그래서 사영 공간이 사용하는 좌표계는 동차좌표계라고 부른다.
$$\frac{y’}{z’} = a\frac{x’}{z’} + b$$ $$ y’ = ax’ + bz’$$
- NDC의 원점 $(0, 0)$
- 카메라로 멀어질수록 투영된 NDC 좌푯값은 원점 $(0, 0)$에 가까워진다.
- 이런 NDC의 원점은 회화의 투시 원근 기법에서 사용하는 소실점(Vanishing point) 에 해당한다.
-
다음은 원근 투영 변환행렬을 사용해서 원근감을 준 코드이다. 또한 입력에 따라 화각을 달리하여 변화되는 모습을 볼 수 있다.
-
(1) 클립 좌표 값 얻기
class CameraObject
{
public:
FORCEINLINE Matrix4x4 GetPerspectiveMatrix() const;
private:
float _FOV = 60.f; // 시야각
};
// 원근 투영 행렬 P를 생성한다.
FORCEINLINE Matrix4x4 CameraObject::GetPerspectiveMatrix() const
{
float invA = 1.f / _ViewportSize.AspectRatio();
float d = 1.f / tanf(Math::Deg2Rad(_FOV) * 0.5f);
return Matrix4x4(
Vector4::UnitX * invA * d,
Vector4::UnitY * d,
Vector4(0.f, 0.f, -1.f, 0.f),
Vector4(0.f, 0.f, 0, 1.f)
);
}
// 게임 로직을 담당하는 함수
void SoftRenderer::Update3D(float InDeltaSeconds)
{
// 게임 로직에서 사용하는 모듈 내 주요 레퍼런스
GameEngine& g = Get3DGameEngine();
const InputManager& input = g.GetInputManager();
// 게임 로직의 로컬 변수
static float moveSpeed = 500.f;
static float fovSpeed = 100.f; // 시야각 조절 속도
static float minFOV = 15.f; // 최소 시야각
static float maxFOV = 150.f; // 최대 시야각
// 게임 로직에서 사용할 게임 오브젝트 레퍼런스
GameObject& goPlayer = g.GetGameObject(PlayerGo);
CameraObject& camera = g.GetMainCamera();
TransformComponent& playerTransform = goPlayer.GetTransform();
// 입력에 따른 플레이어 트랜스폼의 변경
Vector3 inputVector = Vector3(input.GetAxis(InputAxis::XAxis), input.GetAxis(InputAxis::YAxis), input.GetAxis(InputAxis::ZAxis)).GetNormalize();
playerTransform.AddPosition(inputVector * moveSpeed * InDeltaSeconds);
// 입력에 따른 카메라 트랜스폼의 변경
// deltaFOV로 시야각 변화량을 계산하고
// 최소, 최댓값 사이로 시야각을 설정한다.
camera.SetLookAtRotation(playerTransform.GetPosition());
float deltaFOV = input.GetAxis(InputAxis::WAxis) * fovSpeed * InDeltaSeconds;
camera.SetFOV(Math::Clamp(camera.GetFOV() + deltaFOV, minFOV, maxFOV));
}
// 렌더링 로직을 담당하는 함수
void SoftRenderer::Render3D()
{
// 렌더링 로직에서 사용하는 모듈 내 주요 레퍼런스
const GameEngine& g = Get3DGameEngine();
auto& r = GetRenderer();
const CameraObject& mainCamera = g.GetMainCamera();
// 배경에 기즈모 그리기
DrawGizmo3D();
// 렌더링 로직의 로컬 변수
const Matrix4x4 vMatrix = mainCamera.GetViewMatrix();
const Matrix4x4 pMatrix = mainCamera.GetPerspectiveMatrix();
for (auto it = g.SceneBegin(); it != g.SceneEnd(); ++it)
{
const GameObject& gameObject = *(*it);
if (!gameObject.HasMesh() || !gameObject.IsVisible())
{
continue;
}
// 렌더링에 필요한 게임 오브젝트의 주요 레퍼런스를 얻기
const Mesh& mesh = g.GetMesh(gameObject.GetMeshKey());
const TransformComponent& transform = gameObject.GetTransform();
// 원근투영행렬 * 뷰행렬 * 모델링행렬
// (1) 결과는 클립 좌표의 값이겠다.
Matrix4x4 finalMatrix = pMatrix * vMatrix * transform.GetModelingMatrix();
// 메시 그리기
DrawMesh3D(mesh, finalMatrix, gameObject.GetColor());
if (gameObject == PlayerGo)
{
// 플레이어의 위치
r.PushStatisticText("Player: " + transform.GetPosition().ToString());
}
}
r.PushStatisticText("Camera: " + mainCamera.GetTransform().GetPosition().ToString());
r.PushStatisticText("FOV : " + std::to_string(mainCamera.GetFOV()));
}
- (2) 클립 좌표 값을 NDC로 변환하고, (3) 해상도 크기로 늘려주기.
// 삼각형을 그리는 함수
void SoftRenderer::DrawTriangle3D(std::vector<Vertex3D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
auto& r = GetRenderer();
const GameEngine& g = Get3DGameEngine();
// (2) 클립 좌표를 NDC 좌표로 변경
for (auto& v : InVertices)
{
// 무한 원점인 경우, 약간 보정해준다.
if (v.Position.Z == 0.f) v.Position.Z = SMALL_NUMBER;
float invZ = 1.f / v.Position.Z;
v.Position.X *= invZ;
v.Position.Y *= invZ;
v.Position.Z *= invZ;
}
// 백페이스 컬링
Vector3 edge1 = (InVertices[1].Position - InVertices[0].Position).ToVector3();
Vector3 edge2 = (InVertices[2].Position - InVertices[0].Position).ToVector3();
Vector3 faceNormal = -edge1.Cross(edge2);
Vector3 viewDirection = Vector3::UnitZ;
if (faceNormal.Dot(viewDirection) >= 0.f)
{
return;
}
// (3) NDC 좌표를 화면 좌표로 늘리기
for (auto& v : InVertices)
{
v.Position.X *= _ScreenSize.X * 0.5f;
v.Position.Y *= _ScreenSize.Y * 0.5f;
}
LinearColor finalColor = _WireframeColor;
if (InColor != LinearColor::Error)
{
finalColor = InColor;
}
r.DrawLine(InVertices[0].Position, InVertices[1].Position, finalColor);
r.DrawLine(InVertices[0].Position, InVertices[2].Position, finalColor);
r.DrawLine(InVertices[1].Position, InVertices[2].Position, finalColor);
}
깊이 값 #
- 깊이(Depth) 값의 필요성
- 우리에게 보이는 화면은 결국 2차원 평면이므로 가장 카메라에서 멀리 있는, 나중에 그린 물체가 앞에 보일 수 밖에 없다.
- 이 문제를 해결하기 위해서는 카메라로부터 물체가 얼마나 떨어졌는지에 대한 깊이 값이 필요하다.
- 깊이 값을 추가하면 2차원 평면이었던 NDC영역이 3차원으로 확장된다. 여기서 깊이값의 범위는 동일하게 $[-1, 1]$ 이다.
- 절두체(Frustum)
- 카메라에 가장 가까이 있는, 깊이 값이 $-1$인 평면을 근평면(Near plane) 이라고 한다.
- 반대로 가장 멀리에 있는, 깊이 값이 $1$인 평면을 원평면(Far plane) 이라고 한다.
- 사영 공간을 근평면과 원평면으로 잘라서 만들어진 부분을 절두체라고 한다.
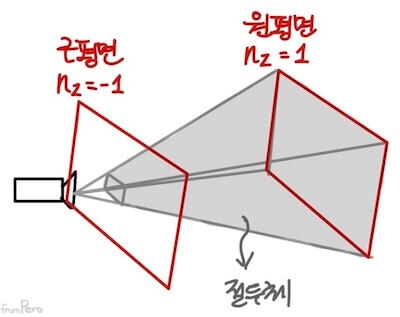
- 절두체로 생성되는 3차원의 NDC영역의 범위는 다음과 같다. NDC 깊이 값은 멀어질수록 증가하기 때문에 왼손좌표계를 사용한다.
- 원근 투영 행렬에 깊이 값을 넣기 위해 3행을 4행으로 옮기고 3행을 깊이값을 구하는 용도로 변경하자.
- 뷰 공간의 점이 $\vec{v} = (v_x, v_y, v_z, 1)$일 때 다음과 같이 구할 수 있다.
$$ P \cdot \vec{v} = \begin{bmatrix} \frac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ ? & ? & ? & ? \\ 0 & 0 & -1 & 0 \end{bmatrix} \begin{bmatrix} v_x \\ v_y \\ v_z \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{d}{a} \cdot v_x \\ d \cdot v_y \\ ? \\ -v_z\end{bmatrix}$$
- 여기서 깊이 값은 뷰 좌표계의 $x$, $y$축과 직교하므로 영향을 받지 않는다. 그러므로 3행의 앞의 두 요소는 $0$으로 설정할 수 있겠다.
$$ P \cdot \vec{v} = \begin{bmatrix} \frac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0 & 0 & ? & ? \\ 0 & 0 & -1 & 0 \end{bmatrix} \begin{bmatrix} v_x \\ v_y \\ v_z \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{d}{a} \cdot v_x \\ d \cdot v_y \\ ? \\ -v_z\end{bmatrix}$$
- 이제 여기에서 근평면과 원평면의 값을 사용해보자.
- 근평면에 있는 점을 $P_1$, 원평면에 있는 점을 $P_2$라고 하자.
- 그리고 카메라부터 근평면까지의 거리를 $n$, 원평면까지의 거리를 $f$라고 하자.
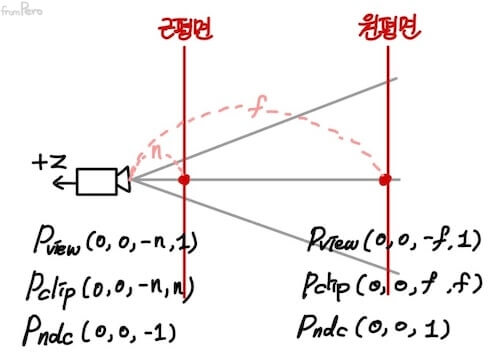
- 근평면의 경우
- 뷰 공간의 좌표는 $(0, 0, -n, 1)$이 된다.
- 근평면은 깊이 값의 시작부분이므로 NDC좌표의 $(0, 0, -1)$에 대응한다.
- 따라서 다음과 같이 만들어진다. $$ P_1 = \begin{bmatrix} \frac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0 & 0 & ? & ? \\ 0 & 0 & -1 & 0 \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ -n \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ ? \\ n \end{bmatrix}$$
- 클립 좌표의 경우 세번째 원소를 마지막 네번째 원소로 나눈 값이 NDC의 세번째 원소인 $-1$이 되므로, $?$는 $-n$이 된다.
$$ P_1 = \begin{bmatrix} \frac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0 & 0 & ? & ? \\ 0 & 0 & -1 & 0 \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ -n \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ -n \\ n \end{bmatrix}$$
- 원평면의 경우
- 동일한 방식으로 다음과 같이 구할 수 있겠다. $$ P_2 = \begin{bmatrix} \frac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0 & 0 & ? & ? \\ 0 & 0 & -1 & 0 \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ -f \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ f \\ f \end{bmatrix}$$
- 여기서 두행렬의 3행과 뷰 공간의 점을 내적한 후 수식을 정리하면 다음과 같이 최종 원근 투영 행렬을 구할 수 있다.
$$ P = \begin{bmatrix} \frac{d}{a} & 0 & 0 & 0\\ 0 & d & 0 & 0\\ 0 & 0 & \frac{n + f}{n - f} & \frac{2nf}{n - f} \\ 0 & 0 & -1 & 0 \end{bmatrix} $$
- 위에서 봤던 예제 코드에 깊이 값까지 계산하는 코드를 추가하였다.
class CameraObject
{
public:
FORCEINLINE Matrix4x4 GetPerspectiveMatrix() const;
FORCEINLINE Matrix4x4 GetPerspectiveViewMatrix() const;
private:
float _FOV = 60.f;
float _NearZ = 5.5f;
float _FarZ = 5000.f;
};
// 깊이 값을 계산하는 최종 원근 투영 행렬
FORCEINLINE Matrix4x4 CameraObject::GetPerspectiveMatrix() const
{
// 투영 행렬. 깊이 값의 범위는 -1~1
float invA = 1.f / _ViewportSize.AspectRatio();
float d = 1.f / tanf(Math::Deg2Rad(_FOV) * 0.5f);
// 근평면과 원평면에 반대 부호를 붙여서 계산
float invNF = 1.f / (_NearZ - _FarZ);
float k = (_FarZ + _NearZ) * invNF;
float l = 2.f * _FarZ * _NearZ * invNF;
return Matrix4x4(
Vector4::UnitX * invA * d,
Vector4::UnitY * d,
Vector4(0.f, 0.f, k, -1.f),
Vector4(0.f, 0.f, l, 0.f)
);
}
// 원근투영 행렬과 뷰 행렬을 곱한 행렬
FORCEINLINE Matrix4x4 CameraObject::GetPerspectiveViewMatrix() const
{
// 뷰 행렬 관련 요소
Vector3 viewX, viewY, viewZ;
GetViewAxes(viewX, viewY, viewZ);
Vector3 pos = _Transform.GetPosition();
float zPos = viewZ.Dot(pos);
// 투영 행렬 관련 요소
float invA = 1.f / _ViewportSize.AspectRatio();
float d = 1.f / tanf(Math::Deg2Rad(_FOV) * 0.5f);
float dx = invA * d;
float invNF = 1.f / (_NearZ - _FarZ);
float k = (_FarZ + _NearZ) * invNF;
float l = 2.f * _FarZ * _NearZ * invNF;
return Matrix4x4(
Vector4(dx * viewX.X, d * viewY.X, k * viewZ.X, -viewZ.X),
Vector4(dx * viewX.Y, d * viewY.Y, k * viewZ.Y, -viewZ.Y),
Vector4(dx * viewX.Z, d * viewY.Z, k * viewZ.Z, -viewZ.Z),
Vector4(-dx * viewX.Dot(pos), -d * viewY.Dot(pos), -k * zPos + l, zPos)
);
}
// 렌더링 로직을 담당하는 함수
void SoftRenderer::Render3D()
{
// 렌더링 로직에서 사용하는 모듈 내 주요 레퍼런스
const GameEngine& g = Get3DGameEngine();
auto& r = GetRenderer();
const CameraObject& mainCamera = g.GetMainCamera();
// 배경에 기즈모 그리기
DrawGizmo3D();
// 원근 투영 행렬 * 뷰행렬의 결과 행렬
const Matrix4x4 pvMatrix = mainCamera.GetPerspectiveViewMatrix();
for (auto it = g.SceneBegin(); it != g.SceneEnd(); ++it)
{
const GameObject& gameObject = *(*it);
if (!gameObject.HasMesh() || !gameObject.IsVisible())
{
continue;
}
// 렌더링에 필요한 게임 오브젝트의 주요 레퍼런스를 얻기
const Mesh& mesh = g.GetMesh(gameObject.GetMeshKey());
const TransformComponent& transform = gameObject.GetTransform();
// 원근 투영 행렬 * 뷰행렬 * 모델링 행렬
Matrix4x4 finalMatrix = pvMatrix * transform.GetModelingMatrix();
// 메시 그리기
DrawMesh3D(mesh, finalMatrix, gameObject.GetColor());
if (gameObject == PlayerGo)
{
// 플레이어 관련 정보 나타내기
// 플레이어의 클립 좌표 구하기
Vector4 clippedPos = pvMatrix * Vector4(transform.GetPosition());
// 클립 좌표의 네번째 요소 -Vz
float cameraDepth = clippedPos.W;
// -Vz가 0인 경우 0이 되지 않도록 보완해주기
if (cameraDepth == 0) cameraDepth = SMALL_NUMBER;
// NDC의 깊이값 계산: 클립좌표의 세번째 요소 / 클립좌표의 네번째 요소
float ndcZ = clippedPos.Z / cameraDepth;
r.PushStatisticText("Player: " + transform.GetPosition().ToString());
r.PushStatisticText("Depth: " + std::to_string(ndcZ));
r.PushStatisticText("Distance: " + std::to_string(clippedPos.W));
}
}
r.PushStatisticText("Camera: " + mainCamera.GetTransform().GetPosition().ToString());
r.PushStatisticText("FOV : " + std::to_string(mainCamera.GetFOV()));
}
원근 보정 매핑 #
- 문제가 한 가지 있다. 투영 전과 투영 후의 무게중심좌표가 달라져서 텍스처 매핑을 하면 이상하게 나온다.
- 예를 들어, 사영 공간의 점 $P_1$, $P_3$가 카메라 시야각에 걸쳐 있고, 카메라 정면에 위치한 점 $P_2$가 있다고 하자.
- 그러면 $P_2$를 투영한 후에 NDC좌표는 투영 평면의 정 중앙에 위치하며 무게중심좌표가 $0.5$가 된다.
- 하지만 투영 전을 보면 $0.5$보다 더 작은 값이 나올 것이다.
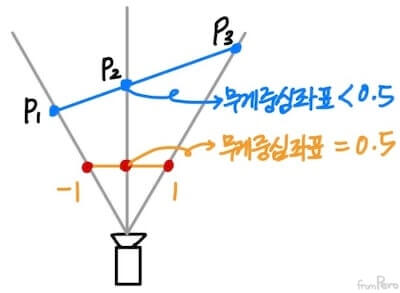
- 이것은 변환 과정에서 사영 공간의 마지막 요소인 $-v_z$로 나눴기 때문이다. 이런 반비례 관계때문에 이런 문제가 발생하였다.
- 따라서 NDC에서의 무게중심좌표가 아니라 투영 전 사영 공간의 무게중심좌표를 써야 한다.
- 만약 NDC에서의 무게중심좌표를 가지고 투영 전 사영 공간의 무게중심좌표를 알아낼 수 있다면 좋을 것이다.
- 투영 보정 보간(Perspective correction interpolation)
- 투영 전의 무게중심좌표 값을 계산해서 텍스처를 매핑하는 것이다.
- 반비례 함수 $y = -\frac{1}{x}$가 가진 성질을 먼저 살펴보자.
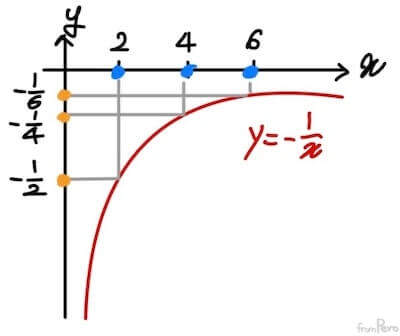
- $x$축에 위치한 세 수 중에서 가운데 위치한 $4$의 무게중심좌표 $a$는 다음 식에 의해 구할 수 있으며 $a = 0.5$가 된다.
$$ 4 = a \cdot 2 + (1-a) \cdot 6 $$
- 그리고 $y$축에서 가운데 위치한 $-\frac{1}{4}$의 경우 다음과 같으며 $a = 0.25$가 된다.
$$ -\frac{1}{4} = a \cdot - \frac{1}{2} + (1 - a) \cdot -\frac{1}{6}$$
- 이 둘을 다음과 같이 나타내 보자.
$$ x’ = t_1 \cdot x_1 + t_2 \cdot x_2 (t_1 + t_2 = 1) $$ $$ y’ = q_1 \cdot y_1 + q_2 \cdot y_2 (q_1 + q_2 = 1) $$
- $x’$, $y’$는 서로 반비례 관계이므로 $y$값을 $\frac{1}{x}$로 나타낼 수 있다.
$$ \frac{1}{x’} = q_1 \cdot \frac{1}{x_1} + q_2 \cdot \frac{1}{x_2} $$ $$ x’ = \frac{1}{ q_1 \cdot \frac{1}{x_1} + q_2 \cdot \frac{1}{x_2} }$$
- 이 식을 다시 변환해보자.
$$ q_1 \cdot \frac{x’}{x_1} + q_2 \cdot \frac{x’}{x_2} = 1 = t_1 + t_2 $$
- 따라서 다음 식을 도출할 수 있다.
$$ t_1 = \frac{x’}{x_1}q_1 $$ $$ t_2 = \frac{x’}{x_2}q_2 $$
- 위의 식이 올바르게 적용되는지 확인해보자.
- $y$축에서 $q_1 = \frac{1}{4}, q_2 = \frac{3}{4}$ 이다.
- $x$축에서 $x_1 = 2, x_2 = 6, x’ = 4$이다.
- 따라서 $t_1$, $t_2$가 $0.5$임을 알 수 있다.
$$t_1 = \frac{x’}{x_1}q_1 = \frac{4}{2} \cdot \frac{1}{4} = 0.5$$ $$t_2 = \frac{x’}{x_2}q_2 = \frac{4}{6} \cdot \frac{3}{4} = 0.5$$
- 두 점이 아닌 삼각형의 세 점으로 확장하고, $x$를 $-z$로 치환하면 최종 투영 보정 보간식을 얻을 수 있다.
$$ z’ = \frac{1}{ q_1 \cdot \frac{1}{z_1} + q_2 \cdot \frac{1}{z_2} + q_3 \cdot \frac{1}{z_3}}$$ $$ t_1 = \frac{z’}{z_1}q_1 $$ $$ t_2 = \frac{z’}{z_2}q_2 $$ $$ t_3 = \frac{z’}{z_3}q_3 $$
- 다음은 원근 보정 매핑(Perspective correction mapping) 을 하는 코드이다.
// 삼각형을 그리는 함수
void SoftRenderer::DrawTriangle3D(std::vector<Vertex3D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
//...
// 두 점이 화면 밖을 벗어나는 경우 클리핑 처리
lowerLeftPoint.X = Math::Max(0, lowerLeftPoint.X);
lowerLeftPoint.Y = Math::Min(_ScreenSize.Y, lowerLeftPoint.Y);
upperRightPoint.X = Math::Min(_ScreenSize.X, upperRightPoint.X);
upperRightPoint.Y = Math::Max(0, upperRightPoint.Y);
// 각 정점마다 보존된 뷰 공간의 z값: 1/z1, 1/z2, 1/z3
float invZ0 = 1.f / InVertices[0].Position.W;
float invZ1 = 1.f / InVertices[1].Position.W;
float invZ2 = 1.f / InVertices[2].Position.W;
// 삼각형 영역 내 모든 점을 점검하고 색칠
for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
{
for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
{
ScreenPoint fragment = ScreenPoint(x, y);
Vector2 pointToTest = fragment.ToCartesianCoordinate(_ScreenSize);
Vector2 w = pointToTest - InVertices[0].Position.ToVector2();
float wdotu = w.Dot(u);
float wdotv = w.Dot(v);
float s = (wdotv * udotv - wdotu * vdotv) * invDenominator;
float t = (wdotu * udotv - wdotv * udotu) * invDenominator;
float oneMinusST = 1.f - s - t;
if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
{
// 투영보정에 사용할 공통 분모: z'
float z = invZ0 * oneMinusST + invZ1 * s + invZ2 * t;
float invZ = 1.f / z;
Vector2 targetUV = (
InVertices[0].UV * oneMinusST * invZ0 + // q1/z1
InVertices[1].UV * s * invZ1 + // q2/z2
InVertices[2].UV * t * invZ2 // q3/z3
) * invZ;
r.DrawPoint(fragment, FragmentShader3D(mainTexture.GetSample(targetUV), LinearColor::White));
}
}
}
}
깊이 버퍼 #
- 깊이 테스팅(Depth testing)
- 이전에 깊이 값을 구해서 멀리 떨어진 물체를 먼저 그렸다. 하지만 물체가 겹쳐 있다면 어떻게 할 것인가?
- 근본적인 해결방법은 게임 오브젝트 단위가 아니라, 삼각형의 픽셀단위로 깊이를 비교하고, 가까운 곳에 있는 픽셀만 그리는 것이다.
- 화면의 픽셀마다 깊이 값을 별도로 보관하는 깊이 버퍼(Depth buffer)를 사용하면 되겠다.
- 현재 깊이 값을 깊이 버퍼에 저장된 값과 비교해서 현재 깊이 값이 작은 경우에만 픽셀을 찍도록 하면 된다. 이 작업을 깊이 테스팅이라고 한다.
- 삼각형을 구성하는 세 점의 깊이 값 $z_1$, $z_2$, $z_3$ (범위: $[-1, 1]$)으로부터 각 픽셀의 무게중심좌표 $q_1$, $q_2$, $q_3$ (범위: $[0, 1]$)을 사용해서 픽셀의 깊이 값을 구할 수 있겠다.
- 아래 수식에서 $z’$ 값의 범위는 $[-1, 1]$이 된다.
$$ z’ = q_1 \cdot z_1 + q_2 \cdot z_2 + q_3 \cdot z_3$$
// 삼각형을 그리는 함수
void SoftRenderer::DrawTriangle3D(std::vector<Vertex3D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
//...
// 삼각형 영역 내 모든 점을 점검하고 색칠
for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
{
for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
{
//...
if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
{
//...
// 깊이 버퍼 테스팅
if (toggleDepthTesting)
{
// 깊이 테스팅
float newDepth = InVertices[0].Position.Z * oneMinusST + InVertices[1].Position.Z * s + InVertices[2].Position.Z * t;
float prevDepth = r.GetDepthBufferValue(fragment);
if (newDepth < prevDepth)
{
// 픽셀을 처리하기 전 깊이 값을 버퍼에 보관
r.SetDepthBufferValue(fragment, newDepth);
}
else
{
// 이미 앞에 무언가 그려져있으므로 픽셀그리기는 생략
continue;
}
}
Vector2 targetUV = (InVertices[0].UV * oneMinusST * invZ0 + InVertices[1].UV * s * invZ1 + InVertices[2].UV * t * invZ2) * invZ;
r.DrawPoint(fragment, FragmentShader3D(mainTexture.GetSample(targetUV), LinearColor::White));
}
}
}
}
- 깊이 값은 카메라에서 멀어질 수록 급격히 $1$과 가까워진다.
- 이것은 NDC공간에서 깊이 값의 변화가 $y = -\frac{1}{x}$로 비선형 형태를 띠기 때문이다.
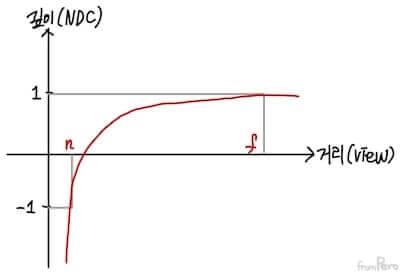
- 따라서 이를 해결하기 위해 이전에 다뤘던 원근 보정 매핑 방식을 이용해서 뷰 공간의 깊이 값을 활용할 수 있겠다.
$$ z’ = \frac{1}{ q_1 \cdot \frac{1}{z_1} + q_2 \cdot \frac{1}{z_2} + q_3 \cdot \frac{1}{z_3}}$$
- 다음은 깊이 값을 $[0, 1]$범위로 바꾸어서 그 값에 따라 흑백 이미지로 출력하는 예제이다.
- 뷰 공간에서 절두체가 가지는 깊이의 범위는 원평면에서 근평면을 뺀 $f-n$이다.
- 따라서 이때 사용할 깊이값은 다음과 같다.
$$c_{depth} = \frac{z’ - n}{f - n}$$
// 삼각형을 그리는 함수
void SoftRenderer::DrawTriangle3D(std::vector<Vertex3D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
auto& r = GetRenderer();
const GameEngine& g = Get3DGameEngine();
const CameraObject& mainCamera = g.GetMainCamera();
// 카메라의 근평면과 원평면 값
float n = mainCamera.GetNearZ();
float f = mainCamera.GetFarZ();
//...
// 삼각형 영역 내 모든 점을 점검하고 색칠
for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
{
for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
{
//...
if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
{
//...
if (IsDepthBufferDrawing())
{
float grayScale = (newDepth + 1.f) * 0.5f;
if (useLinearVisualization)
{
// 카메라로부터의 거리에 따라 균일하게 증감하는 흑백 값으로 변환
grayScale = (invZ - n) / (f - n);
}
// 뎁스 버퍼 그리기
r.DrawPoint(fragment, LinearColor::White * grayScale);
}
else
{
// 최종 보정보간된 UV 좌표
Vector2 targetUV = (InVertices[0].UV * oneMinusST * invZ0 + InVertices[1].UV * s * invZ1 + InVertices[2].UV * t * invZ2) * invZ;
r.DrawPoint(fragment, FragmentShader3D(mainTexture.GetSample(targetUV), LinearColor::White));
}
}
}
}
}