[게임 수학] Chapter 11. 외적: 3차원 공간의 분석과 응용
Table of Contents
이득우의 게임 수학 책을 읽고 공부한 노트입니다.
벡터의 외적 #
- 벡터의 외적(Cross product)
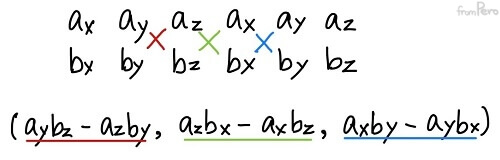
$$\vec{a} = (a_x, a_y, a_z), \vec{b} = (b_x, b_y, b_z)$$ $$\vec{a} \times \vec{b} = (a_yb_z - a_zb_y, a_zb_x - a_xb_z, a_xb_y - a_yb_x)$$
- Chapter 10에서 설명했던 회전의 순환 순서 $x$→$y$→$z$→$x$에 맞춰 벡터를 순서대로 나열하는 형태이며, 결과는 언제나 3차원 벡터가 된다.
- $x$성분의 결과를 만들기 위해 $x$와 관련없는 나머지 두 성분의 $y$와 $z$를 결합해서 만든다. 항상 같은 성분만 사용하는 내적과 대비된다.
외적의 성질 #
- 교환법칙이 성립하지 않는다.
- 위의 식을 살펴보면 교환법칙이 성립하지 않는 뺄셈을 사용한 것을 알 수 있다.
$$\vec{a} \times \vec{b} \neq \vec{b} \times \vec{a}$$
- 뺄셈처럼, 순서를 바꿔서 연산하면 반대 방향이 나온다.
$$\vec{a} \times \vec{b} = -\vec{b} \times \vec{a}$$
- 결합법칙이 성립하지 않는다.
$$\vec{a} \times (\vec{b} \times \vec{c}) \neq (\vec{a} \times \vec{b}) \times \vec{c}$$
- 덧셈에 대한 분배법칙은 성립한다.
$$\vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}$$
| 내적 | 외적 | |
|---|---|---|
| 계산 결과 | 스칼라 | 벡터 |
| 교환법칙 | 성립함 | 성립하지 않음 |
| 결합법칙 | 성립하지 않음 | 성립하지 않음 |
| 분배법칙 | 성립함 | 성립함 |
| 연산 방법 | 같은 위치의 요소만 사용 | 다른 위치의 요소만 사용 |
평행성 판별 #
- 동일한 벡터를 내적하면? 벡터 크기를 제곱한 값이 나왔다. (Chapter 7 참고)
- 동일한 벡터를 외적하면? 그 결과는 항상 영벡터가 나온다.
$$\vec{a} \times \vec{a} = (a_ya_z - a_za_y, a_za_x - a_xa_z, a_xa_y - a_ya_x) = (0, 0, 0)$$
- 이것은 반대 방향의 벡터 $-\vec{a}$를 외적하는 경우에도 동일하다.
$$\vec{a} \times -\vec{a} = (-a_ya_z + a_za_y, -a_za_x + a_xa_z, -a_xa_y + a_ya_x) = (0, 0, 0)$$
- 평행하지만 크기가 다른 벡터 $k \cdot \vec{a}$를 사용해도 마찬가지이다.
$$\vec{a} \times (k \cdot \vec{a}) = (ka_ya_z - ka_za_y, ka_za_x - ka_xa_z, ka_xa_y - ka_ya_x) = (0, 0, 0)$$
- 따라서, 평행한 두벡터를 외적하면 항상 영벡터가 나온다는 걸 알 수 있다.
- 외적의 성질을 알아보기 위해서, 벡터 $\vec{b}$를 벡터 $\vec{a}$에 수평인 벡터 $\vec{b_{\parallel}}$와 수직인 벡터 $\vec{b_{\perp}}$로 분리하여 그 둘의 덧셈으로 나타내보자.
$$\vec{b} = \vec{b_{\parallel}} + \vec{b_{\perp}}$$
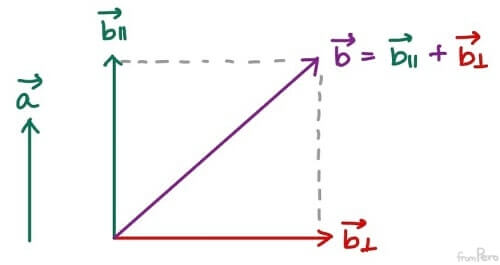
- 이것을 $\vec{a} \times \vec{b}$에 적용하면 다음과 같다.
$$\vec{a} \times \vec{b} = \vec{a} \times (\vec{b_{\parallel}} + \vec{b_{\perp}})= \vec{a} \times \vec{b_{\parallel}} + \vec{a} \times \vec{b_{\perp}}$$
- 여기서 $\vec{a} \times \vec{b_{\parallel}}$는 서로 평행해서 영벡터이므로 다음과 같아진다.
$$\vec{a} \times \vec{b} = \vec{a} \times \vec{b_{\perp}}$$
- 이처럼 외적은 상대방에 직교하는 벡터 성분만 사용되는 성질이 있다.
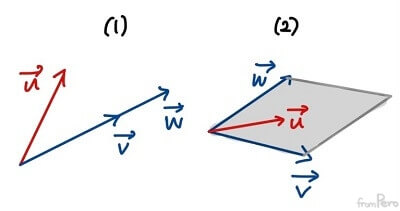
- 아래 그림을 보면, (1)과 같이 두 벡터의 사잇각이 크면 직교 성분 $\vec{b_{\perp}}$의 크기는 커지고, 반대로 (2)와 같이 사잇각이 작으면 $\vec{b_{\perp}}$의 크기는 작아진다.
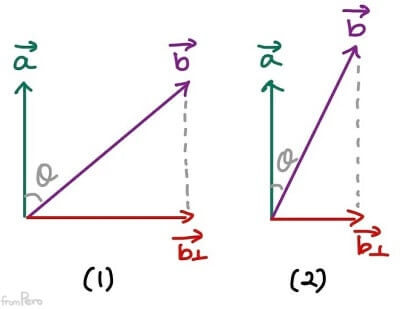
- 직교성분인 $\vec{b_{\perp}}$의 크기는 $\sin$함수에 비례하므로, 외적의 크기도 $\sin$함수에 비례할 것이다.
- 이것을 수식으로 확인해보기 위해 세 가지 연산 $|\vec{a} \times \vec{b}|^2$, $(|\vec{a}||\vec{b}|)^2$, $(\vec{a} \cdot \vec{b})^2$를 전개해보면 다음과 같은 관계를 도출할 수 있다. (풀이 생략) $$|\vec{a} \times \vec{b}|^2 = (|\vec{a}||\vec{b}|)^2 - (\vec{a} \cdot \vec{b})^2$$ $$ = (|\vec{a}||\vec{b}|)^2 - (|\vec{a}||\vec{b}|\cos\theta)^2$$ $$ = (|\vec{a}||\vec{b}|)^2 (1 - \cos^2\theta)$$ $$ = (|\vec{a}||\vec{b}|)^2 \sin^2\theta$$ $$|\vec{a} \times \vec{b}| = |\vec{a}||\vec{b}| |\sin\theta|$$
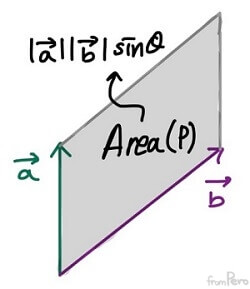
- 이처럼 벡터 외적의 크기는 $\sin$함수에 비례하는 것을 알 수 있다.
- 또한 이것은 두 벡터가 만드는 평행사변형의 넓이와 같다.
| 내적 | 외적 | |
|---|---|---|
| 판별성 ($0$이 될 때) | 직교성 | 평행성 |
| 삼각함수 | $\cos\theta$ | $\sin\theta$ |
법선 벡터 #
- 두 벡터의 외적에다가 한 가지 벡터를 내적하면 어떻게 될까?
$$\vec{a} \cdot (\vec{a} \times \vec{b}) = a_xa_yb_z - a_xa_zb_y + a_ya_zb_x - a_ya_xb_z + a_za_xb_y - a_za_yb_x = 0$$ $$\vec{b} \cdot (\vec{a} \times \vec{b}) = b_xa_yb_z - b_xa_zb_y + b_ya_zb_x - b_ya_xb_z + b_za_xb_y - b_za_yb_x = 0$$
- 그 결과는 늘 $0$이 되며, 이것은 외적 결과값이 두 벡터에 직교한다는 의미가 된다.
-
Chapter 3에서 말했듯이, 선형 독립 관계를 가지는 두 벡터의 선형 결합은 평면을 만든다. 그렇다면 벡터의 외적은 그 평면이 향하는 방향(직교)에 대한 벡터를 만드는 것이다.
- 이 벡터를 법선 벡터 또는 노멀 벡터(Normal vector) 라고 한다.
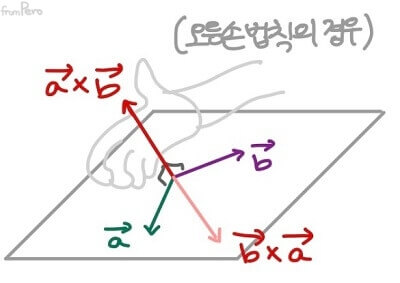
- 외적은 교환법칙이 성립하지 않는다. 따라서 연산의 순서를 바꾸면 반대방향의 법선 벡터가 생성된다.
- 오른손 좌표계를 사용한다면 오른손 법칙을, 왼손 좌표계를 사용한다면 왼손 법칙을 사용해서 법선 벡터의 방향을 파악할 수 있다.
좌우 방향 판별 #
- 월드 공간의 $y$축 $\vec{y} = (0, 1, 0)$에 직교하는 평면에 캐릭터와 몬스터가 놓여 있다.
- 이 때, 캐릭터의 정면을 향하는 시선 벡터 $\vec{f}$와 캐릭터에서 몬스터로 향하는 벡터 $\vec{v}$를 외적하면?
- 결과 벡터는 오른손 법칙의 경우 평면의 위쪽으로 향할 것이다.
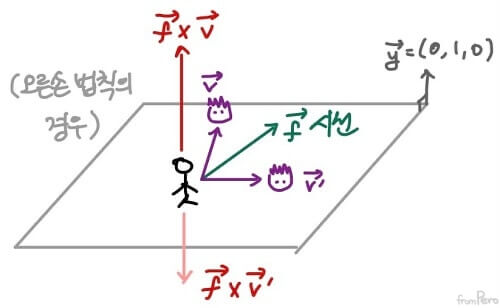
- 외적의 결과 벡터 $\vec{f} \times \vec{v}$에 평면의 위쪽 방향을 나타내는 벡터 $\vec{y}$를 내적하자.
- 두 벡터의 방향이 같으면 양수가 나오고 반대 방향이라면 음수가 나온다.
| 몬스터의 위치 | 판별식의 값 |
|---|---|
| 오른쪽에 있다 | $(\vec{f} \times \vec{v}) \cdot \vec{y} < 0$ |
| 왼쪽에 있다 | $(\vec{f} \times \vec{v}) \cdot \vec{y} > 0$ |
| 정확히 시선 방향과 일치한다 | $(\vec{f} \times \vec{v}) = 0$ |
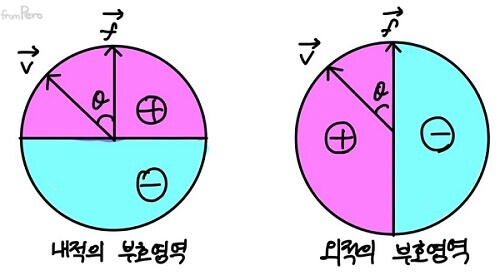
- 이러한 성질은 외적이 $\sin$함수에 비례하는 성질을 가졌기 때문이다.
- 반면, 내적은 $\cos$함수에 비례하기 때문에 앞뒤 판별에 사용된다.
| 내적 | 외적 | |
|---|---|---|
| 방향 판별 | 앞뒤 | 좌우 |
벡터로부터 회전행렬 생성 #
- Chapter 10에서는 오일러 각 방식을 사용해서 카메라의 회전을 지정하였다.
- 이번에는 외적을 사용해보자.
- 그러면 카메라의 시선 벡터 하나를 가지고 카메라를 구성하는 세 가지 로컬 축을 구할 수가 있다.
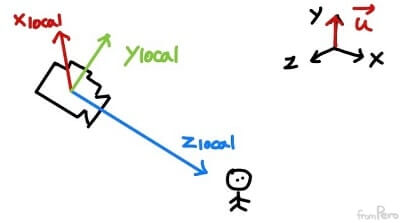
| 로컬 축 | 구하는 법 |
|---|---|
| 로컬 $z$축 | 물체의 위치에서 카메라의 위치를 뺀 후 크기를 $1$로 정규화 시킨 시선 벡터이다. |
| 로컬 $x$축 | 월드 공간의 $y$축(Up vector: 업벡터라고 한다)과 카메라의 로컬 $z$축을 외적한 후 정규화하면 얻을 수 있다. |
| 로컬 $y$축 | 로컬 $z$축과 로컬 $x$축을 외적하면 얻을 수 있다. |
- 따라서 시선 벡터 $\vec{v}$와 업 벡터 $\vec{u}$로부터 다음과 같이 구할 수 있다.
$$\vec{z} = \frac{\vec{v}}{|\vec{v}|}$$ $$\vec{x} = \frac{\vec{v} \times \vec{u}}{|\vec{v} \times \vec{u}|}$$ $$\vec{y} = \vec{x} \times \vec{z}$$
- 그렇다면 카메라 트랜스폼의 회전 행렬 $R$은 로컬 벡터를 열벡터로 지정해서 다음과 같이 생성할 수 있겠다.
$$R = \begin{bmatrix} x_x & y_x & z_x & 0 \\ x_y & y_y & z_y & 0 \\ x_z & y_z & z_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
예외 상황 #
- (1) 카메라의 위쪽방향이 월드 공간의 $y$축과 반대인 경우 (뒤집힌 경우)
- 월드 공간 $y$축과 반대인 $(0, -1, 0)$을 업벡터로 사용해야 한다.
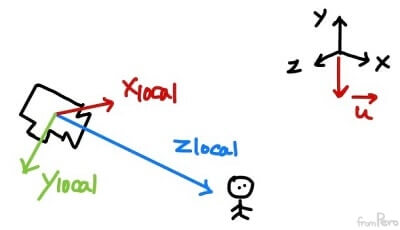
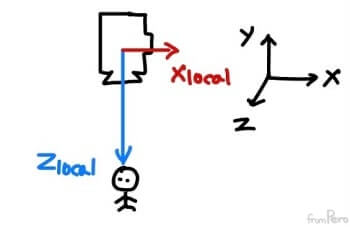
- (2) 카메라의 시선방향이 월드 공간의 $y$축과 평행한 경우
- 이때 업벡터를 월드 공간의 $y$축으로 지정해 버린다면, 로컬 $x$축을 구하기 위해 하는 $\vec{v} \times \vec{u}$에서 두 벡터는 서로 평행하므로 외적의 결과는 $0$이 된다.
- 따라서 로컬 $z$축에 직교하는 로컬 $x$축의 값을 수동으로 지정해야 한다.
// 목표물의 위치로부터 카메라의 세 로컬 축을 구해서 트랜스폼에 반영한다.
// (예외 상황 1) InUp은 카메라가 뒤집힌 경우에는 반대 방향의 월드 Y축이 전달되겠다.
void CameraObject::SetLookAtRotation(const Vector3& InTargetPosition, const Vector3& InUp)
{
Vector3 localX, localY, localZ;
localZ = (InTargetPosition - _Transform.GetPosition()).Normalize();
// (예외 상황 2) 단위 벡터 Z축의 y값이 1과 가깝다는 것은,
// 그 단위벡터와 월드의 Y축(0, 1, 0)이 서로 거의 평행하다는 것이다.
// 이렇게 시선 방향인 Z과 월드 Y축이 평행한 경우에는 외적 결과가 0이 나와버리므로,
// 임의로 X축을 만들어준다.
if (Math::Abs(localZ.Y) >= (1.f - SMALL_NUMBER))
{
localX = Vector3::UnitX; // 로컬 X 좌표 값을 임의로 지정한다.
}
else
{
localX = InUp.Cross(localZ).Normalize();
}
localY = localX.Cross(localX);
// 최종 계산된 세 로컬 축을 카메라의 트랜스폼에 반영한다.
_Transform.SetLocalAxes(localX, localY. localZ);
}
렌더링 계산량을 줄여주는 백페이스 컬링 #
- 백페이스 컬링(Backface culling)
- 카메라와 마주보지 않는 메시의 뒷면은 그리지 않고 건너뛰는 것이다. 덕분에 빠르게 렌더링할 수 있겠다.
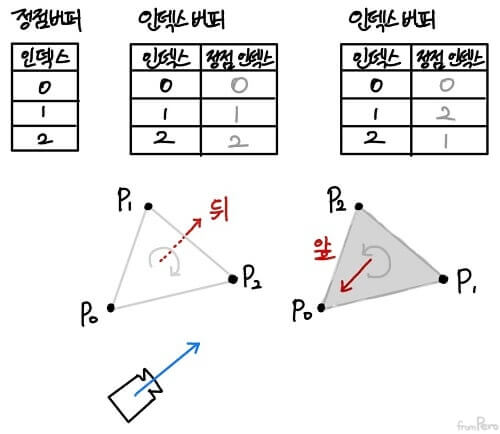
- 삼각형의 세 점을 지정하는 인덱스 버퍼에는 점의 순서가 나열되어있다. 이것을 활용하면 외적을 사용해서 삼각형이 향하는 방향을 파악할 수 있다.
- 삼각형의 방향과 카메라의 시선 방향을 내적해서 그 결과 값이 음수라면, 방향이 마주보고 있다는 것이므로 그린다.
- 나머지 경우에는 두 방향이 같은 방향을 바라보는 것이므로 그리지 않는다.
백페이스 컬링 구현 코드 #
- 삼각형의 면이 향하는 법선 벡터
$$\vec{n} = \vec{P_0P_1} \times \vec{P_0P_2}$$
- 뷰 공간에서 카메라가 바라보는 시선이 $-z$축이므로 $(0, 0, -1)$과 내적을 하고, 그 값이 음수일 때만 그린다.
$$(n_x, n_y, n_z) \cdot (0, 0, -1) < 0$$
void SoftRenderer::DrawTriangle3D(std::vector<Vertex3D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
auto& r = GetRenderer();
const GameEngine& g = Get3DGameEngine();
if (useBackfaceCulling)
{
// 백페이스 컬링
Vector3 edge1 = (InVertices[1].Position - InVertices[0].Position).ToVector3();
Vector3 edge2 = (InVertices[2].Position - InVertices[0].Position).ToVector3();
Vector3 faceNormal = edge1.Cross(edge2);
Vector3 viewDirection = -Vector3::UnitZ;
if (faceNormal.Dot(viewDirection) >= 0.f)
{
// 뒷 면이면 그리지 않는다.
return;
}
}
LinearColor finalColor = _WireframeColor;
if (InColor != LinearColor::Error)
{
finalColor = InColor;
}
r.DrawLine(InVertices[0].Position, InVertices[1].Position, finalColor);
r.DrawLine(InVertices[0].Position, InVertices[2].Position, finalColor);
r.DrawLine(InVertices[1].Position, InVertices[2].Position, finalColor);
}
오일러 각의 문제를 해결하는 로드리게스 회전 공식 #
- Chapter 10에서 본 것처럼, 오일러 각은 짐벌락 현상이 발생하고 회전 보간이 어렵다는 문제가 있었다.
- 이 문제들은 축-각 회전(Axis-Angle rotation)을 사용해서 해결할 수 있다.
- 임의의 축에 직교하는 평면에서 회전을 하는 방법이다.
- 아래 그림과 같을 때 $\vec{u’}$를 구해보자.
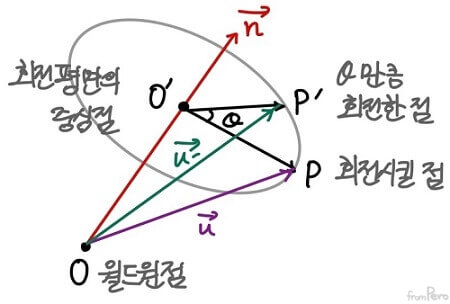
- 먼저, 점 $P$의 좌표가 $P = (x, y, z, 1)$이라면 $\vec{u} = P - O$이므로 $\vec{u} = (x, y, z, 0)$라고 할 수 있겠다.
- $\vec{OO’}$의 경우에는 Chapter 7에서 본 투영 벡터를 구하는 공식으로 구할 수 있다.
- 이것을 간단히 $\vec{v}$라고 부르자. $$\vec{v} = (\vec{u} \cdot \hat{n}) \cdot \hat{n}$$
- 그렇다면 $\vec{O’P}$의 경우에는 $\vec{u} - \vec{v}$로 구할 수 있다.
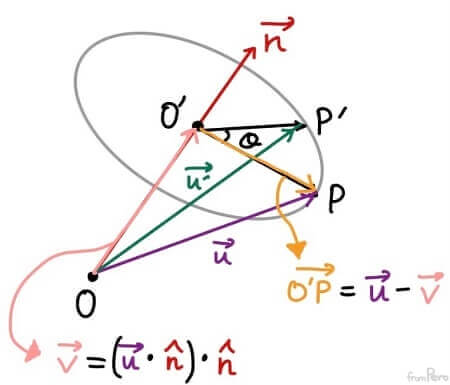
- 이번에는 회전 평면을 위에서 내려다 보자.
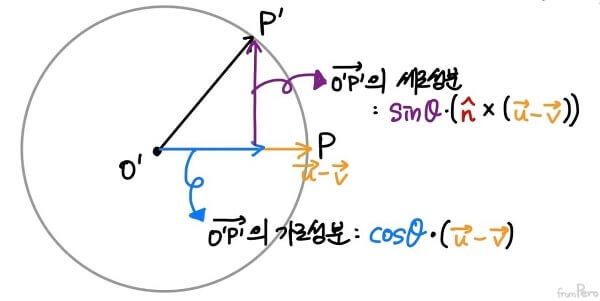
- 벡터 $\vec{O’P’}$의 가로 성분에 해당하는 벡터는 다음과 같이 구할 수 있다.
$$\cos\theta \cdot (\vec{u} - \vec{v})$$
- 벡터 $\vec{O’P’}$의 세로 성분에 해당하는 벡터도 구해보자.
- 세로 성분과 같은 방향을 향하는 벡터를 $\vec{O’Q}$라고 하자. 이것은 법선 벡터 $\hat{n}$와 벡터 $\vec{OP’}$를 외적해서 얻을 수 있다.
$$\vec{O’Q} = \hat{n} \times (\vec{u} - \vec{v})$$
- 여기에 $\sin\theta$를 곱하면 세로 성분에 대한 벡터를 얻을 수 있다.
$$\sin\theta \cdot (\hat{n} \times (\vec{u} - \vec{v}))$$
- 따라서 다음과 같이 벡터 $\vec{O’P’}$를 계산할 수 있겠다. $$\vec{O’P’} = \cos\theta \cdot (\vec{u} - \vec{v}) + \sin\theta \cdot (\hat{n} \times (\vec{u} - \vec{v}))$$ $$ = \cos\theta \cdot (\vec{u} - \vec{v}) + \sin\theta \cdot (\hat{n} \times \vec{u} - \hat{n} \times \vec{v})$$
- $\hat{n}$과 $\vec{v}$는 평행하므로 $\hat{n} \times \vec{v}$는 $0$이므로 다음과 같이 정리된다. $$\vec{O’P’} = \cos\theta \cdot (\vec{u} - \vec{v}) + \sin\theta \cdot (\hat{n} \times \vec{u})$$
- 이제 우리의 목표인 $\vec{u’}$를 구해보자.
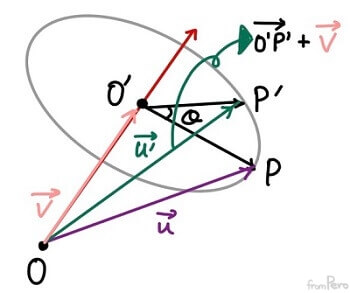
- 이것은 $\vec{O’P’}$에다가 $\vec{v}$를 더해서 얻을 수 있다.
$$\vec{u’} = \vec{v} + \cos\theta \cdot (\vec{u} - \vec{v}) + \sin\theta \cdot (\hat{n} \times \vec{u})$$
- 이제 $\vec{v}$를 $(\vec{u} \cdot \hat{n}) \cdot \hat{n}$로 치환하면 최종 수식이 유도된다.
$$\vec{u’} = \cos\theta \cdot \vec{u} + (1- \cos\theta)(\vec{u} \cdot \hat{n})\cdot \hat{n} + \sin\theta \cdot (\hat{n} \times \vec{u})$$
- 이 공식은 프랑스 수학자 로드리게스가 1840년에 발표했으며, 그의 이름을 인용해서 로드리게스 회전 공식(Rodrigues’ rotation formula)이라고 한다.
// 메시를 그리는 함수
void SoftRenderer::DrawMesh3D(const Mesh& InMesh, const Matrix4x4& InMatrix, const Vector3& InScale, const LinearColor& InColor)
{
size_t vertexCount = InMesh.GetVertices().size();
size_t indexCount = InMesh.GetIndices().size();
size_t triangleCount = indexCount / 3;
// 렌더러가 사용할 정점 버퍼와 인덱스 버퍼로 변환
std::vector<Vertex3D> vertices(vertexCount);
std::vector<size_t> indice(InMesh.GetIndices());
for (size_t vi = 0; vi < vertexCount; ++vi)
{
vertices[vi].Position = Vector4(InMesh.GetVertices()[vi]);
if (InMesh.HasColor())
{
vertices[vi].Color = InMesh.GetColors()[vi];
}
if (InMesh.HasUV())
{
vertices[vi].UV = InMesh.GetUVs()[vi];
}
}
// 정점 변환 진행
for (Vertex3D& v : vertices)
{
float sin = 0.f, cos = 0.f;
Math::GetSinCos(sin, cos, thetaDegree);
Vector3 u = v.Position.ToVector3(); // 원점에서 정점으로 향하는 벡터 u. 계산의 편의를 위해 4차원 벡터의 마지막 요소는 생략했다.
float udotn = u.Dot(n);
Vector3 ncrossu = n.Cross(u);
// 스케일을 적용한 후 로드리게스 공식으로 회전을 적용한다.
Vector3 result = Vector3(u * cos + n * (1.f - cos) * udotn + ncrossu * sin) * InScale;
// 그다음 뷰 행렬(InMatrix로 전달됨)을 적용한다.
v.Position = InMatrix * Vector4(result);
}
// 삼각형 별로 그리기
for (int ti = 0; ti < triangleCount; ++ti)
{
int bi0 = ti * 3, bi1 = ti * 3 + 1, bi2 = ti * 3 + 2;
std::vector<Vertex3D> tvs = { vertices[indice[bi0]] , vertices[indice[bi1]] , vertices[indice[bi2]] };
size_t triangles = tvs.size() / 3;
for (size_t ti = 0; ti < triangles; ++ti)
{
size_t si = ti * 3;
std::vector<Vertex3D> sub(tvs.begin() + si, tvs.begin() + si + 3);
DrawTriangle3D(sub, InColor, FillMode::Color);
}
}
}
- 로드리게스 회전 공식을 활용하면 오일러 각으로 구현하기 어려운 임의의 축에 대한 회전 변환을 수행할 수 있다.
- 하지만, 행렬로의 변환이 어려워서 지금까지 구축했던 렌더링 파이프라인에 연동하기가 까다롭다.
- 그래서 게임 엔진에서는 동일한 기능을 제공하지만 간결하고, 행렬로 변환이 용이한 사원수 (Chapter 16)를 사용한다.
삼중곱 #
- 삼중곱(Triple product) 연산
- 벡터의 외적과 내적을 두 번 연속 사용 하는 연산이다.
- 다음과 같은 경우의 수가 있겠다.
| 경우 | 설명 |
|---|---|
| $\vec{u} \cdot (\vec{v} \cdot \vec{w})$ | 결과 값이 스칼라이므로 제외한다. |
| $\vec{u} \cdot (\vec{v} \times \vec{w})$ | → 스칼라 삼중곱 |
| $\vec{u} \times (\vec{v} \cdot \vec{w})$ | 벡터와 스칼라는 외적할 수 없으므로 연산이 불가능해서 제외한다. |
| $\vec{u} \times (\vec{v} \times \vec{w})$ | → 벡터 삼중곱 |
스칼라 삼중곱 #
- 스칼라 삼중곱(Scalar triple product)
$$\vec{u} \cdot (\vec{v} \times \vec{w})$$
- 왼쪽과 오른쪽 판별 방법과, 백페이스 컬링에 사용했던 공식이 바로 스칼라 삼중곱이었다.
$$(\vec{f} \times \vec{v}) \cdot \vec{y}$$ $$-\hat{z} \cdot (\vec{P_0P_1} \times \vec{P_0P_2})$$
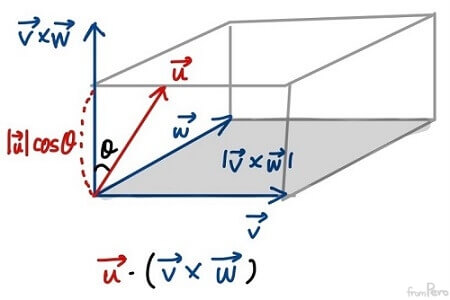
- 임의의 벡터 $\vec{u}$를 법선 벡터 $\vec{v} \times \vec{w}$에 투영한 벡터의 높이는 $|\vec{u}|\cos\theta$이다.
- 여기에 평행사변형의 넓이 $|\vec{v} \times \vec{w}|$를 곱하면 육면체의 부피가 나온다.
$$|\vec{u}||\vec{v} \times \vec{w}|\cos\theta$$
- 이것은 스칼라 삼중곱이 만들어내는 값의 절댓값과 동일하다.
$$|\vec{u} \cdot (\vec{v} \times \vec{w})| = |\vec{u}||\vec{v} \times \vec{w}|\cos\theta$$
- 따라서 스칼라 삼중곱의 절댓값은 세 벡터가 만드는 평행육면체(Parallelepiped)의 부피를 의미한다는 것을 알 수 있다.
- 이 세 백터에서 바닥에 해당하는 두 벡터를 다른 벡터로 변경해도 최종 육면체의 부피 값은 변하지 않아서 삼중곱의 결과는 동일하다.
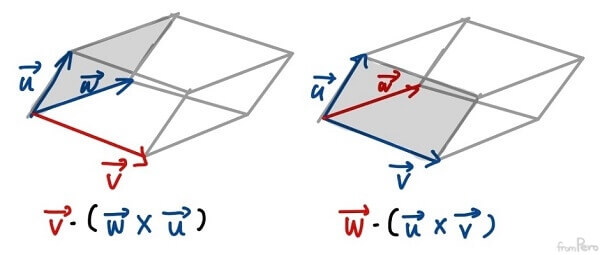
- 따라서 다음과 같은 성질을 도출할 수 있다.
$$\vec{u} \cdot (\vec{v} \times \vec{w}) = \vec{v} \cdot (\vec{w} \times \vec{u}) = \vec{w} \cdot (\vec{u} \times \vec{v})$$
- 스칼라 삼중곱이 $0$이 아니면 세 백터는 모두 선형 독립의 관계를 가진다.
- Chapter 5에서 보았던 행렬식의 절댓값은 평행사변형의 넓이였다. 이것은 평면에서 평행사변형을 이루는 두 벡터가 서로 선형 독립의 관계를 가지는지 판단하는 수식이었다.
- 외적으로 생성된 벡터의 크기는 평행사변형의 넓이와 같다.
- 따라서 스칼라 삼중곱은 3차원 공간의 세 벡터가 모두 선형 독립의 관계를 가지는지 판단하는 판별식으로 생각할 수 있다.
- 스칼라 삼중곱이 $0$이 나오는 경우
- (1) 외적의 결과가 영벡터이므로 스칼라 삼중곱이 $0$이 된다.
- (2) 외적의 결과로 만들어진 법선 벡터에 벡터 $\vec{u}$가 직교하므로 이의 내적은 $0$이 된다. 따라서 스칼라 삼중곱은 $0$이 된다.
벡터 삼중곱 #
- 벡터 삼중곱(Vector triple product)
$$\vec{u} \times (\vec{v} \times \vec{w})$$
- 벡터 삼중곱은 다음과 같은 성질을 지니는 데 이것을 삼중곱 전개(Triple product expansion) 또는 라그랑주 공식(Lagrange’s formula) 이라고 한다.
$$\vec{u} \times (\vec{v} \times \vec{w}) = (\vec{u} \cdot \vec{w}) \cdot \vec{v} - (\vec{u} \cdot \vec{v}) \cdot \vec{w}$$
- 이것을 직접 확인해보면 다음과 같다. (풀이 생략)
$$(\vec{u} \times (\vec{v} \times \vec{w}))_x = v_x(\vec{u} \cdot \vec{w}) - w_x(\vec{u} \cdot \vec{v})$$ $$(\vec{u} \times (\vec{v} \times \vec{w}))_y = v_y(\vec{u} \cdot \vec{w}) - w_y(\vec{u} \cdot \vec{v})$$ $$(\vec{u} \times (\vec{v} \times \vec{w}))_z = v_z(\vec{u} \cdot \vec{w}) - w_z(\vec{u} \cdot \vec{v})$$
- 이 식의 우변은 $a\vec{v} + b\vec{w}$형태의 선형 결합식이므로, 벡터 삼중곱으로 만들어지는 벡터는 두 벡터 $\vec{v}$, $\vec{w}$가 만드는 평면에 속함을 알 수 있다.
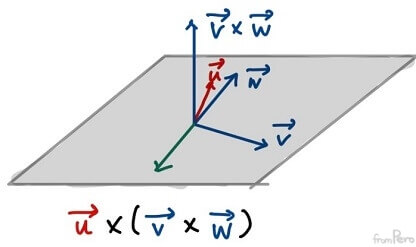
- 벡터 삼중곱은 2차원에서 동일 평면에 있는 직교 벡터를 구하는 데도 유용하게 쓸 수 있다.
$$(\vec{u} \times \vec{v}) \times \vec{u}$$