[게임 수학] Chapter 10. 3차원 공간: 입체 공간의 생성
Table of Contents
이득우의 게임 수학 책을 읽고 공부한 노트입니다.
3차원 공간의 설계 #
- 3차원 공간의 설계 방법은 $x$축에서 $y$축 방향으로 손을 감았을 때 $z$축이 어느쪽 손의 엄지 손가락의 방향과 일치하는가에 따라 나뉜다.
- 오른손 좌표계(Right-handed coordinate system)
- 왼손 좌표계(Left-handed coordinate system)
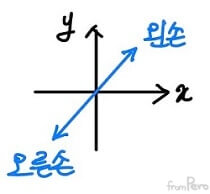
- 프로그램 마다 각 축의 용도를 다르게 설정한다.
- 3DS맥스는 $z$업 오른손 좌표계이고, 유니티는 $y$업, 언리얼은 $z$업 왼손 좌표계이다.
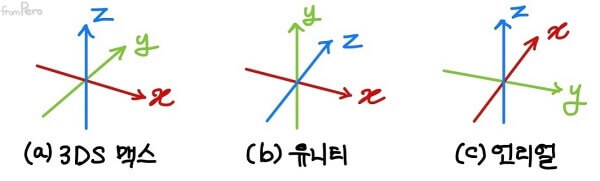
- (저자가 제시한) 우리가 사용할 좌표계는 유니티 좌표계에서 $z$축의 방향이 반대인 형상이다.
- $y$업 오른손 좌표계
3차원 공간의 트랜스폼 #
- 3차원 공간 역시 이동 변환을 위해서 한 차원 더 늘어난 4차원 공간을 사용한다.
$$S = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$ $$T = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
- 3차원 공간의 회전 변환은?
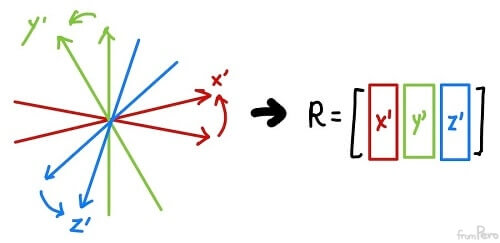
- 세 가지 표준기저벡터가 동일한 크기와 직교성을 유지한 상태로 함께 움직여야한다.
- 회전변환으로 달라진 세 표준기저벡터값을 열벡터로 꽂아 넣어 회전변환행렬 $R$을 만들 수 있을 것이다.
오일러 각 #
- 오일러 각(Euler’s angle)
- 3차원 공간에서 물체가 놓인 방향을 3개의 각을 사용해서 표시하는 방법이다.
- 오일러 각은 표준기저벡터를 중심으로해서 회전한 각의 크기로 나타낸다.
$$(\theta_x, \theta_y, \theta_z)$$
- 하지만 소프트웨어마다 $x$, $y$, $z$축의 용도가 다르다는 문제가 있다.
- 예를 들면 언리얼에서 사용하는 $x$축 회전은 유니티의 $x$축 회전과 다르게 동작하므로, 언리얼 엔진에서의 오일러 각 정보를 그대로 유니티 엔진으로 넘겨서 사용할 수 없다.
- 이런 문제를 해결하기 위해 회전의 움직임으로 회전 동작을 구분하는 방법을 사용한다.
- 요, 롤, 피치의 움직임으로 오일러 각을 지정하면, 서로 다른 좌표계를 사용하는 프로그램 간에도 데이터를 쉽게 변환할 수 있다.
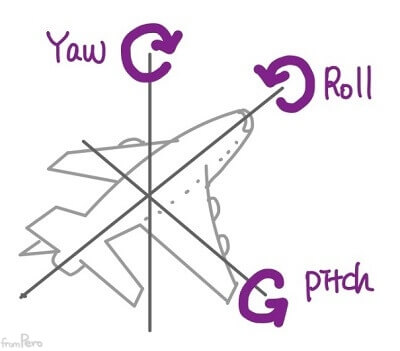
| 회전 | 방향 | 유니티 | 언리얼 |
|---|---|---|---|
| 요(Yaw) | 위 | $y$ | $z$ |
| 롤(Roll) | 앞 | $z$ | $x$ |
| 피치(Pitch) | 오른쪽 | $x$ | $y$ |
- 오일러 각에서 회전은 표준기저벡터를 중심으로 진행되는 세 번의 연속적인 회전을 의미한다. 따라서 다음과 같이 각 기저축의 회전행렬을 구할 수 있겠다.
- 3차원 공간에서는 $x$→$y$→$z$→$x$→$y$의 순서로 세 축이 순환된다.
- $x$축 회전은 $yz$평면의 회전을 의미한다.
$$R_x = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix}$$
- $y$축 회전은 $zx$평면의 회전을 의미한다. (위의 순서에 따르므로 $xz$가 아니다)
$$R_y = \begin{bmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{bmatrix}$$
- $z$축 회전은 $xy$평면의 회전을 의미한다.
$$R_z = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}$$
회전행렬의 유도 #
- 각 기저축의 회전행렬을 순서대로 적용해서 최종 회전행렬을 만들어야 한다.
- 어떤 순서로 적용할 것인가에 대한 경우의 수는 다양하다. 그 중에서 언리얼 엔진은 $Roll$→$Pitch$→$Yaw$의 순서를 채택한다. 이 순서로 회전행렬 $R$을 구하면 다음과 같다.
$$ R = R_{yaw} \cdot R_{pitch} \cdot R_{roll} $$
- (저자가 제시한) 우리의 좌표계는 $Roll$→$Pitch$→$Yaw$가 $z$→$x$→$y$에 대응되므로 요, 피치, 롤 각의 값을 $\alpha$, $\beta$, $\gamma$라고 한다면 행렬 곱은 다음과 같이 계산할 수 있다.
$$R_{\alpha} \cdot R_{\beta} \cdot R_{\gamma} = \begin{bmatrix} \cos\alpha & 0 & \sin\alpha \\ 0 & 1 & 0 \\ -\sin\alpha & 0 & \cos\alpha \end{bmatrix} \begin{bmatrix} \cos\beta & 0 & \sin\beta \\ 0 & 1 & 0 \\ -\sin\beta & 0 & \cos\beta \end{bmatrix} \begin{bmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ $$= \begin{bmatrix} \cos\alpha\cos\gamma + \sin\alpha\sin\beta\sin\gamma & -\cos\alpha\sin\gamma + \sin\alpha\sin\beta\cos\gamma & \sin\alpha\cos\beta \\ \cos\beta\sin\gamma & \cos\beta\cos\gamma & -\sin\beta \\ -\sin\alpha\cos\gamma + \cos\alpha\sin\beta\sin\gamma & \sin\alpha\sin\gamma + \cos\alpha\sin\beta\cos\gamma & \cos\alpha\cos\beta \end{bmatrix}$$
- 이렇게 계산한 회전행렬의 열벡터는 표준기저벡터가 회전 변환된 로컬 축을 의미한다. 따라서 다음과 같이 나타낼 수 있겠다.
$$x_{local} = ( \cos\alpha\cos\gamma + \sin\alpha\sin\beta\sin\gamma, \cos\beta\sin\gamma, -\sin\alpha\cos\gamma + \cos\alpha\sin\beta\sin\gamma )$$ $$y_{local} = ( -\cos\alpha\sin\gamma + \sin\alpha\sin\beta\cos\gamma, \cos\beta\cos\gamma, \sin\alpha\sin\gamma + \cos\alpha\sin\beta\cos\gamma )$$ $$z_{local} = ( \sin\alpha\cos\beta, -\sin\beta, \cos\alpha\cos\beta )$$
struct Rotator
{
public:
// 0~360 범위로 각도 값을 바꿔준다.
FORCEINLINE void Clamp()
{
Yaw = GetAxisClampedValue(Yaw);
Roll = GetAxisClampedValue(Roll);
Pitch = GetAxisClampedValue(Pitch);
}
FORCEINLINE float GetAxisClampedValue(float InRotatorValue)
{
float angle = Math::FMod(InRotatorValue, 360.f);
if (angle < 0.f)
{
angle += 360.f;
}
return angle;
}
// 오일러각으로 회전된 3차원 공간의 로컬 축을 계산해서 반환한다.
FORCEINLINE void GetLocalAxes(Vector3& OutRight, Vector3& OutUp, Vector3& OutForward)
{
float cy = 0.f, sy = 0.f, cp = 0.f, sp = 0.f, cr = 0.f, sr = 0.f;
Math::GetSinCos(sy, cy, Yaw);
Math::GetSinCos(sp, cp, Pitch);
Math::GetSinCos(sr, cr, Roll);
OutRight = Vector3( cy * cr + sy * sp * sr, cp * sr, -sy * cr + cy * sp * sr);
OutUp = Vector3(-cy * sr + sy * sp * cr, cp * cr, sy * sr + cy * sp * cr);
OutForward = Vector3( sy * cp, -sp, cy * cp);
}
public:
// 오일러 각을 구성하는 요, 롤, 피치는 각도법을 사용해서 관리한다.
float Yaw. = 0.f;
float Roll = 0.f;
float Pitch = 0.f;
}
- 3차원 공간의 트랜스폼도 회전 변환이 발생할 때마다 로컬 축 데이터를 갱신한다면,
- 로컬 축 벡터가 $\vec{x} = (x_x, x_y, x_z), \vec{y} = (y_x, y_y, y_z), \vec{z} = (z_x, z_y, z_z)$일 때 이들을 열벡터로 꽂아넣어 회전행렬을 구할 수 있다.
$$R = \begin{bmatrix} x_x & y_x & z_x & 0 \\ x_y & y_y & z_y & 0 \\ x_z & y_z & z_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
class TransformComponent
{
public:
// 오일러 각의 정보가 변경되면 항상 Update함수를 호출해서 로컬 축을 갱신한다.
void AddYawRotation(float InDegree) { _Rotation.Yaw += InDegree; Update(); }
void AddRollRotation(float InDegree) { _Rotation.Roll += InDegree; Update(); }
void AddPitchRotation(float InDegree) { _Rotation.Pitch += InDegree; Update(); }
void SetRotation(const Rotator & InRotation) { _Rotation = InRotation; Update(); }
const Vector3& GetLocalX() const { return _Right; }
const Vector3& GetLocalY() const { return _Up; }
const Vector3& GetLocalZ() const { return _Forward; }
// 로컬 축 값을 직접 설정한다.
void SetLocalAxes(const Vector3 & InRight, const Vector3 & InUp, const Vector3 & InForward)
{
_Right = InRight;
_Up = InUp;
_Forward = InForward;
}
private:
FORCEINLINE void Update();
Vector3 _Position = Vector3::Zero;
Rotator _Rotation; // 트랜스폼의 회전을 관리하기 위해 오일러 각 방식의 Rotator 구조체를 사용한다.
Vector3 _Scale = Vector3::One;
Vector3 _Right = Vector3::UnitX;
Vector3 _Up = Vector3::UnitY;
Vector3 _Forward = Vector3::UnitZ;
};
FORCEINLINE void TransformComponent::Update()
{
_Rotation.Clamp(); // 오일러 각의 범위를 0~360 범위로 바꿔준다.
_Rotation.GetLocalAxes(_Right, _Up, _Forward); // 오일러 각으로부터 세 로컬 축 값을 가져와서 로컬 축에 저장한다.
}
3차원 모델링 행렬 #
- 크기, 회전, 이동 변환행렬
$$S = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$ $$R = \begin{bmatrix} x_x & y_x & z_x & 0 \\ x_y & y_y & z_y & 0 \\ x_z & y_z & z_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$ $$T = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
- 모델링 행렬
$$M = T \cdot R \cdot S = \begin{bmatrix} x_xs_x & y_xs_y & z_xs_z & t_x \\ x_ys_x & y_ys_y & z_ys_z & t_y \\ x_zs_x & y_zs_y & z_zs_z & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
// 3차원 모델링 행렬을 생성한다.
FORCEINLINE Matrix4x4 TransformComponent::GetModelingMatrix() const
{
return Matrix4x4(
Vector4( _Right * _Scale.X, false), // 두번째 인자값이 false이면 점이고, 네번째 원소값이 0이 된다.
Vector4( _Up * _Scale.Y, false),
Vector4(_Forward * _Scale.Z, false),
Vector4( _Position, true) // 두번째 인자값이 true이면 벡터이고, 네번째 원소값이 1이 된다.
);
}
카메라 공간 #
- 2차원 카메라를 구현할 때에는 이동 기능만 부여 했지만, 3차원 공간의 카메라에는 이동과 회전 기능을 함께 부여할 것이다.
- 카메라의 경우 크기의 개념이 없기 때문에 크기는 제외한다.
- 카메라 트랜스폼에 저장된 위치값을 $t = (t_x, t_y, t_z)$로 지정하고, 로컬 축 값을 각각 $\vec{x} = (x_x, x_y, x_z), \vec{y} = (y_x, y_y, y_z), \vec{z} = (z_x, z_y, z_z)$로 지정한다면 이동 행렬과 회전 행렬은 다음과 같다.
$$T = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}$$ $$R = \begin{bmatrix} x_x & y_x & z_x & 0 \\ x_y & y_y & z_y & 0 \\ x_z & y_z & z_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
-
Chapter 9에서 보았듯이 카메라의 위치를 기준으로 측정한 월드 원점의 상대 좌표는 역행렬로 구할 수 있다.
- 이동 행렬의 역행렬은 덧셈의 역원인 반대수로 구한다.
- 회전 행렬의 역행렬은 전치행렬로 구한다. (Chapter 5 참고) $$T^{-1} = \begin{bmatrix} 1 & 0 & 0 & -t_x \\ 0 & 1 & 0 & -t_y \\ 0 & 0 & 1 & -t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}$$ $$R^{-1} = \begin{bmatrix} x_x & x_y & x_z & 0 \\ y_x & y_y & y_z & 0 \\ z_x & z_y & z_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
- 순서는?
- 모든 물체의 좌표를 카메라를 중심으로 옮긴 후, 회전을 해야하므로 이동의 역행렬 → 회전의 역행렬 순이다.
- 이것은 트랜스폼의 순서를 바꾸는 것이며, 즉 크기 변환 $S$를 제외한 모델링 행렬의 역행렬이 뷰 행렬이 된다.
$$M^{-1} = (T \cdot R)^{-1} = R^{-1} \cdot T^{-1}$$
- 따라서 뷰 행렬은 다음과 같으며, 마지막 4열은 내적을 사용해서 간단하게 정리할 수 있다.
$$R^{-1} \cdot T^{-1} = \begin{bmatrix} x_x & x_y & x_z & -x \cdot t \\ y_x & y_y & y_z & -y \cdot t \\ z_x & z_y & z_z & -z \cdot t \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
- (저자가 제시한) 우리의 좌표계의 경우 카메라가 양의 $z$축을 바라볼 때,
- 카메라를 기준으로 $x$축이 왼쪽을 향해서 2차원 데카르트 좌표계와 다르게 된다.
- 따라서 $x$축이 오른쪽을 향하도록 $y$축을 기준으로 $180^{\circ}$회전 시켜서 뷰 공간을 구성해야 하겠다.
- 이것을 위해 $x$축 기저와 $z$축 기저를 반전시킨다.
// 카메라 트랜스폼으로부터 x, y, z 로컬 축 값을 얻는다.
FORCEINLINE void CameraObject::GetViewAxes(Vector3& OutViewX, Vector3& OutViewY, Vector3& OutViewZ) const
{
// (x축과 z축을 반전시킨다)
OutViewZ = -_Transform.GetLocalZ();
OutViewY = _Transform.GetLocalY();
OutViewX = -_Transform.GetLocalX();
}
// 뷰 행렬을 얻는다.
FORCEINLINE Matrix4x4 CameraObject::GetViewMatrix() const
{
Vector3 viewX, viewY, viewZ;
GetViewAxes(viewX, viewY, viewZ);
Vector3 pos = _Transform.GetPosition();
return Matrix4x4(
Vector4(Vector3(viewX.X, viewY.X, viewZ.X), false),
Vector4(Vector3(viewX.Y, viewY.Y, viewZ.Y), false),
Vector4(Vector3(viewX.Z, viewY.Z, viewZ.Z), false),
Vector4(-viewX.Dot(pos), -viewY.Dot(pos), -viewZ.Dot(pos), 1.f)
);
}
오일러 각의 특징 #
- 장점
- 오일러 각은 표준기저벡터를 회전축으로 삼아서 회전한 각의 크기를 설정하기 때문에 인터페이스가 직관적이다. 따라서 사용자 입장에서 물체의 회전을 설정하기에 용이하다.
- 행렬을 사용해서 3차원 공간의 회전을 표현하려면 최소 9개의 실수 데이터가 필요하지만, 오일러 각은 3개의 데이터만 있으면 된다. 따라서 적은 용량으로 게임 데이터를 관리할 수 있게 도와준다.
- 단점
- 짐벌락 현상이 발생한다.
- 짐벌락(Gimbal lock) 현상
- 오브젝트의 두 회전 축이 겹쳐서 자유도를 잃는 것을 말한다.
- 짐벌락 참고 영상
- 해결 방법
- 로드리게스 회전 공식 (Chapter 11)
- 사원수 (Chapter 16)
회전 보간의 계산 #
- 회전 보간(Rotational interpolation)
- 카메라의 움직임이나 캐릭터의 애니메이션을 구현할 때는 3차원 공간에서 시작 회전과 끝 회전을 지정하고 시간에 따라 두 회전 사이를 부드럽게 전환하는 기능이 필요할 수 있다. 이를 위해서 중간 회전 값을 계산하는 것을 회전 보간이라고 한다.
- 선형 보간식을 사용해서 중간 회전 값을 얻을 수 있겠다.
$$ \theta’ = (1-t)\theta_{start} + t\theta_{end} $$
- 예를 들어, 동일한 평면 상에서 $15^{\circ}$에서 시작해서 $165^{\circ}$로 끝나는 회전의 $\frac{1}{3}$비율에 해당하는 회전 보간 값은 다음과 같이 구해서 $65^{\circ}$가 된다.
$$\frac{2}{3} \cdot 15^{\circ} + \frac{1}{3} \cdot 165^{\circ} = 65^{\circ}$$
- 선형 보간식이 성립하려면 두 각의 회전 변환을 곱한 결과가 두 각의 합의 회전 변환과 동일해야한다.
$$R_{\beta} \cdot R_{\alpha} = R_{(\alpha + \beta)}$$
- Chapter 5에서 보았듯이 2차원 공간의 회전에서는 위 식이 만족하므로, 선형 보간식을 사용하는 데 문제가 없었다.
- 그렇다면 3차원 공간의 오일러 각 회전에서도 문제가 없을까?
- 두 오일러 각의 회전 변환을 곱한 결과가 두 오일러 각의 합의 회전 변환과 동일한지 보면 되겠다.
- 한 축으로만 회전하는 경우
- 맨 처음에 보았던 회전 행렬을 구하는 식은 다음과 같다. $$ R = R_{yaw} \cdot R_{pitch} \cdot R_{roll}$$
- 만약 $y$축으로 $\alpha$와 $\beta$만큼 회전한다면, 두 각의 회전 변환의 합은 다음과 같다. $$R_{(\alpha + \beta)} = R_{yaw(\alpha + \beta)} \cdot I \cdot I$$ $$ = R_{yaw(\alpha + \beta)}$$
- 다음으로 두 회전 변환의 곱을 보자. $yaw$회전만 수행하므로 $pitch$와 $roll$회전 행렬은 변화가 없는 항등행렬이 된다. $$R_{\beta} \cdot R_{\alpha} = (R_{yaw\beta} \cdot I \cdot I) \cdot (R_{yaw\alpha} \cdot I \cdot I)$$ $$ = R_{yaw\beta} \cdot R_{yaw\alpha}$$ $$ = R_{yaw(\alpha + \beta)}$$
- 이처럼 오일러 각에서 한 축만 사용한다는 것은 결국 2차원 평면에서의 회전과 동일하므로, 선형 보간식을 사용하는 데 문제가 없다.
- 두 축에 대해서 회전하는 경우
- 만약 $x$축과 $y$축에 대해서 $\alpha$와 $\beta$만큼 회전한다면, 두 각의 회전 변환의 합은 다음과 같다. $$R_{(\alpha + \beta)} = R_{yaw(\alpha + \beta)} \cdot R_{pitch(\alpha + \beta)} \cdot I$$ $$= R_{yaw(\alpha + \beta)} \cdot R_{pitch(\alpha + \beta)}$$
- 다음으로 두 회전 변환의 곱은 다음과 같다. $$R_{\beta} \cdot R_{\alpha} = (R_{yaw\beta} \cdot R_{pitch\beta} \cdot I) \cdot (R_{yaw\alpha} \cdot R_{pitch\alpha} \cdot I)$$ $$ = R_{yaw\beta} \cdot R_{pitch\beta} \cdot R_{yaw\alpha} \cdot R_{pitch\alpha}$$ $$ \neq R_{(\alpha + \beta)}$$
- 이처럼 두 축 이상을 사용하는 오일러 각은 선형 보간식을 사용할 수 없다.
- 해결 방법
- 로드리게스 회전 공식 (Chapter 11)
- 사원수 (Chapter 16)