[게임 수학] Chapter 9. 게임 엔진: 콘텐츠를 만드는 기술
Table of Contents
이득우의 게임 수학 책을 읽고 공부한 노트입니다.
게임 엔진의 구성 요소 #
-
게임 엔진의 인터페이스는 게임 콘텐츠가 담기는 게임 공간을 설계하는 작업 공간과, 게임 데이터를 관리하는 작업 공간으로 나뉜다.
공간 이름 하는 일 씬(Scene) 또는
레벨(Level)게임 공간 설계 리소스(Resource) 또는
애셋(Asset)데이터 관리 -
게임엔진은 씬 데이터와 리소스 데이터를 결합해서 최종 게임 화면이 렌더링되로록 설계됐다.
씬의 구조 #
- 게임 오브젝트(GameObject) 또는 액터(Actor)
- 씬 안에서 콘텐츠를 구성하는 기본단위이다.
- 크기, 회전, 위치로 구성된 트랜스폼(Transform)의 정보를 사용해서 관리한다.
- 이 트랜스폼 정보에 모델링 행렬을 사용해서 렌더링할 물체의 정점을 변환한다.
모델링 행렬의 설계 #
-
트랜스폼의 크기, 회전, 이동 데이터는 다음과 같다.
분류 데이터 크기 ($S$) 2차원 벡터 $(s_x, s_y)$ 회전 ($R$) 각 $\theta$ 이동 ($T$) 2차원 벡터 $(t_x, t_y)$ -
위 데이터는 크기, 회전, 이동에 대한 세 가지 아핀 변환행렬에 대응된다.
$$S = \begin{bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ $$R = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ $$T = \begin{bmatrix} 1 & 0 & a\\ 0 & 1 & b \\ 0 & 0 & 1 \end{bmatrix}$$
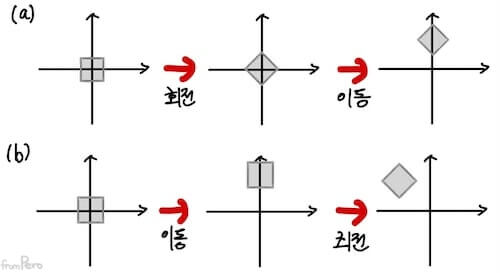
- 그렇다면 아핀 변환을 어떤 순서로 적용해야 할까?
- 회전과 이동변환을 할 경우 아래처럼 순서에 따라서 다른 결과가 나온다. 이것은 회전 대신 크기변환을 해도 마찬가지이다. 따라서 이동변환은 가장 마지막에 해야하겠다.
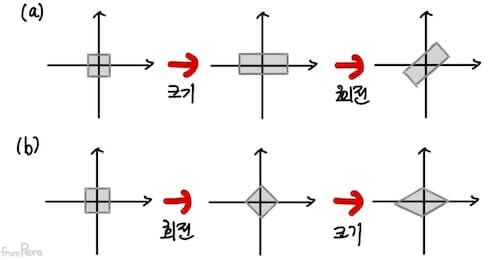
- 이동변환을 제외하면 크기변환과 회전변환이 남는다. 크기와 회전변환을 할 경우에도 순서에 따라서 다른 결과가 나온다. Chapter 7에서 보았듯이 회전변환은 물체의 형태를 그대로 보존해주는 강체 변환(Rigid Transform)이기 때문에 회전변환을 나중에 해서 형태를 유지하는 것이 사용자 입장에서 직관적인 변환이겠다.
- 따라서 아핀 변환의 순서는 크기 → 회전 → 위치순서로 이뤄지며 행렬곱으로 나타내면 다음과 같다. (열 기준 행렬으로 설명한다. 따라서 변환의 순서는 오른쪽에서 왼쪽으로 진행된다.)
$$T \cdot R \cdot S$$
- 이 3가지 변환을 수행하는 합성행렬인 모델링 행렬(Modeling matrix) 은 다음과 같다.
$$M = T \cdot R \cdot S = \begin{bmatrix} \cos\theta \cdot s_x & -\sin\theta \cdot s_y & t_x \\ \sin\theta \cdot s_x & \cos\theta \cdot s_y & t_y \\ 0 & 0 & 1 \end{bmatrix}$$
로컬 공간과 로컬 축 #
- 로컬 공간(Local space)
- Chapter 8에서 보았듯이, 하나의 물체를 표현하기 위해서 만들어진 메시 데이터는 자신만의 공간에서 물체를 구성하는 각 정점의 위치 정보가 저장된다. 이렇게 물체의 정보를 담기 위해 부여한 공간을 로컬 공간이라고 한다.
- 월드 공간(World space)
- 게임 콘텐츠는 단일 물체가 아니라 여러가지 물체를 모아서 하나의 배경을 만든다. 이럴 때 사용하는 새로운 공간을 월드 공간이라고 한다.
- 예를 들어, 비행기 게임을 만든다고 하자. 그러면 월드 공간을 중심으로 설정된 비행기의 위치좌표가 필요하다. 또한 앞으로 나아가는 비행기의 방향을 조종하려면 월드 공간과 무관하게 비행기가 바라보는 방향 정보도 필요할 것이다.
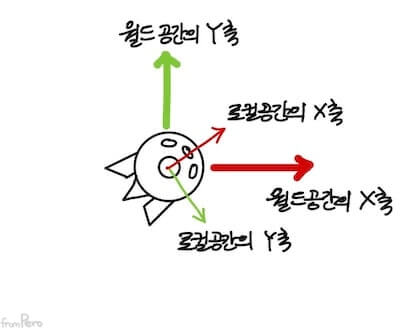
- 로컬 축(Local Axis)
- 이렇게 물체를 기준으로 설정된 방향 정보를 로컬 축이라고 한다.
- 로컬 축 정보는 로컬 공간의 기저벡터와 동일한 값을 가진다.
- 게임 엔진은 월드의 $X$, $Y$, $Z$축과 구분하기 위해 각 로컬 축의 이름을 다음과 같이 부른다.
로컬 축 로컬 축의 이름 $+X$ 라이트벡터 (Right Vector) $+Y$ 업벡터 (Up Vector) $+Z$ 포워드벡터 (Forward Vector)
- 트랜스폼의 이동과 크기 정보가 변경되더라도 게임 오브젝트가 보는 방향은 변함이 없기 때문에, 로컬 축 정보는 오직 회전 정보에만 영향을 받는다.
- 게임 오브젝트에 새로운 회전 값 $\theta$가 설정되면 로컬 축을 구성하는 표준기저벡터도 이에 따라 변한다.
- $e_1$이 변화된 값을 $\vec{r}$로, $e_2$가 변화된 값을 $\vec{u}$로 표현하면 그 값은 다음과 같다.
$$\vec{r} = (\cos\theta, \sin\theta)$$ $$\vec{u} = (-\sin\theta, \cos\theta)$$
- 여기서 로컬축 벡터의 원소를 각각 $\vec{r} = (r_x, r_y)$, $\vec{u} = (u_x, u_y)$로 지정하면?
- 아핀 회전 변환행렬은 삼각함수 대신 로컬 축 벡터를 사용해 생성할 수 있다. 따라서 모델링 행렬 역시 삼각함수 대신 로컬 축 정보를 사용해 계산할 수 있다.
$$M = T \cdot R \cdot S = \begin{bmatrix} r_x \cdot s_x & u_x \cdot s_y & t_x \\ r_y \cdot s_x & u_y \cdot s_y & t_y \\ 0 & 0 & 1 \end{bmatrix}$$
class TransformComponent
{
// 회전하면 로컬 축을 갱신한다.
void SetRotation(float InDegree) { _Rotation = InDegree; Update(); }
void AddRotation(float InDegree) { _Rotation += InDegree; Update(); }
// ...
private:
Vector2 _Position = Vector2::Zero;
Vector2 _Rotation = 0.f;
Vector2 _Scale = Vector2::One;
Vector2 _Right = Vector2::UnityX; // e1
Vector2 _Up = Vector2::UnityY; // e2
};
// 열벡터를 사용해서 모델링 행렬을 만든다.
FORCEINLINE Matrix3x3 TransformComponent::GetModelingMatrix() const
{
return Matrix3x3(
Vector3(_Scale.X * _Right.X, _Scale.X * _Right.Y, 0.f),
Vector3(_ScaleY. * _Up.X, _ScaleY. * _Up.Y, 0.f),
Vector3(_Position.X, _Position.Y, 1.f)
);
}
// sin cos함수를 이용해서 현재 회전 정보에 맞는 로컬 축 벡터를 갱신한다.
FORCEINLINE void TransformComponent::Update()
{
float sin, cos;
Math::GetSinCos(sin, cos, _Rotation); // 발생한 회전의 sin, cos 값을 얻는다.
_Right = Vector2(cos, sin); // e1
_Up = Vector2(-sin, cos); // e2
}
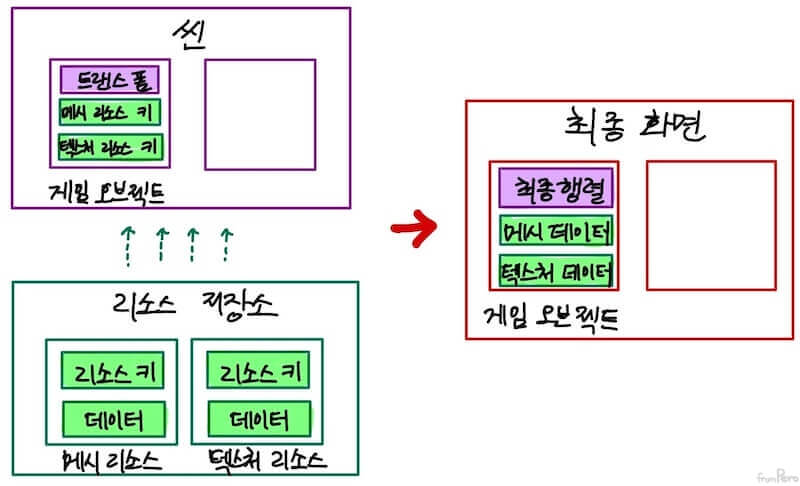
리소스 관리 #
- 월드 공간에 동일한 게임 오브젝트를 여러 개 배치한다고 하자.
- 모델링 행렬을 사용해서 로컬 공간 정보를 월드 공간 정보로 변환하여 트랜스폼 정보를 설정해야할 것이다.
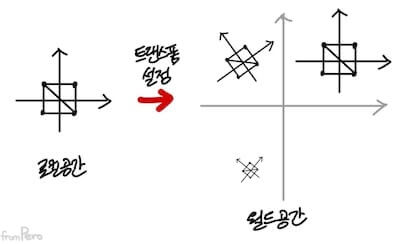
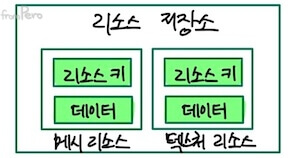
- 여기서 각각의 게임 오브젝트들은 각자의 트랜스폼 정보를 포함하고 있다. 그렇다면 리소스 데이터는 어떨까?
- 용량이 큰 메시 정보를 모두 각각 가지고 있다면 메모리 공간이 낭비될 것이다. 따라서 리소스 데이터는 여러 게임 오브젝트들이 함께 사용할 수 있는 공유 자원의 형태로 관리하는 것이 바람직하다.
- 리소스 저장소(Resource repository)
- 씬과 무관하게 별도로 리소스를 모아두는 저장소이다.
- 게임 오브젝트는 리소스의 키 값만 저장하며, 이것을 통해서 리소스에 접근한다.
게임 엔진의 워크플로우 #
- 워크플로우(Workflow)
- 실행의 흐름이다.
- 게임 엔진의 워크플로우는 크게 씬을 완성하는 과정, 완성된 씬으로부터 화면을 그려내는 과정으로 나뉜다.
- (저자가 제작한) 게임 엔진의 워크플로우
| 순서 | 단계 | 설명 |
|---|---|---|
| 1 | 리소스 로딩 단계 | 메시, 텍스처 같은 리소스는 게임을 진행하면서 불러들이기에는 데이터 양이 크기 때문에 게임 시작 전에 미리 불러들여서 메모리에 올려둬야 안정적으로 게임을 진행할 수 있다. LoadResources() |
| 2 | 씬 구축 단계 | 게임 오브젝트의 트랜스폼 정보가 설정되고, 리소스 정보가 게임 오브젝트에 연결된다.LoadScene2D() |
| 3 | 게임 로직 단계 | 프레임마다 게임 오브젝트의 트랜스폼 값을 변경한다.Update2D() |
| 4 | 렌더링 로직 단계 | 트랜스폼 정보와 리소스 데이터를 활용해서 최종화면을 그린다.Render2D() |
// 1. 리소스 로딩 단계
// 메시
const std::size_t GameEngine::QuadMesh = std::hash<std::string>()("SM_Quad");
// 텍스처
const std::size_t GameEngine::BaseTexture = std::hash<std::string>()("Base");
const std::string GameEngine::CharacterTexturePath("CKMan.png");
bool GameEngine::LoadResources()
{
// 사각형 메시 데이터 객체를 생성하고 QuadMesh 키를 부여한다.
Mesh& quadMesh = CreateMesh(GameEngine::QuadMesh);
constexpr float squareHalfSize = 0.5f;
constexpr int vertexCount = 4;
constexpr int triangleCount = 2;
constexpr int indexCount = triangleCount * 3;
auto& v = quadMesh.GetVertices(); // 정점 버퍼
auto& i = quadMesh.GetIndices(); // 인덱스 버퍼
auto& uv = quadMesh.GetUVs(); // UV 값
v = {
Vector2(-squareHalfSize, -squareHalfSize),
Vector2(-squareHalfSize, squareHalfSize),
Vector2(squareHalfSize, squareHalfSize),
Vector2(squareHalfSize, -squareHalfSize)
};
uv = {
Vector2(0.125f, 0.75f),
Vector2(0.125f, 0.875f),
Vector2(0.25f, 0.875f),
Vector2(0.25f, 0.75f)
};
i = {
0, 2, 1, 0, 3, 2
};
// 텍스처 객체를 생성하고 BaseTexture 키를 부여한다.
Texture& baseTexture = CreateTexture(GameEngine::BaseTexture, GameEngine::CharacterTexturePath);
// ...
}
// 2. 씬 구축 단계
// 게임 오브젝트 목록
static const std::string PlayerGo("Player");
// 최초 씬 로딩을 담당하는 함수
void SoftRenderer::LoadScene2D()
{
// 최초 씬 로딩에서 사용하는 모듈 내 주요 레퍼런스
auto& g = Get2DGameEngine();
// 플레이어의 생성과 설정
constexpr float playerScale = 30.f;
GameObject& goPlayer = g.CreateNewGameObject(PlayerGo); // 게임 오브젝트를 생성한다.
goPlayer.SetMesh(GameEngine::QuadMesh); // 메시 키를 설정한다.
goPlayer.GetTransform().SetScale(Vector2::One * playerScale); // 최초 트랜스폼을 설정한다.
goPlayer.SetColor(LinearColor::Red);
// 100개의 배경 게임 오브젝트 생성과 설정
char name[64];
constexpr float squareScale = 20.f;
std::mt19937 generator(0);
std::uniform_real_distribution<float> dist(-1000.f, 1000.f);
for (int i = 0; i < 100; ++i)
{
std::snprintf(name, sizeof(name), "GameObject%d", i);
GameObject& newGo = g.CreateNewGameObject(name);
newGo.GetTransform().SetPosition(Vector2(dist(generator), dist(generator)));
newGo.GetTransform().SetScale(Vector2::One * squareScale);
newGo.SetMesh(GameEngine::QuadMesh);
newGo.SetColor(LinearColor::Blue);
}
}
// 3. 게임 로직 단계
// 게임 로직을 담당하는 함수
void SoftRenderer::Update2D(float InDeltaSeconds)
{
// 게임 로직에서 사용하는 모듈 내 주요 레퍼런스
auto& g = Get2DGameEngine();
const InputManager& input = g.GetInputManager();
// 게임 로직의 로컬 변수
static float moveSpeed = 200.f;
static float rotateSpeed = 180.f;
static float scaleMin = 15.f;
static float scaleMax = 30.f;
static float scaleSpeed = 180.f;
// 플레이어에 대한 주요 레퍼런스
GameObject& goPlayer = g.GetGameObject(PlayerGo);
TransformComponent& transform = goPlayer.GetTransform();
// 입력에 따른 플레이어 위치와 크기의 변경
float newScale = Math::Clamp(transform.GetScale().X + scaleSpeed * input.GetAxis(InputAxis::ZAxis) * InDeltaSeconds, scaleMin, scaleMax);
transform.SetScale(Vector2::One * newScale);
transform.AddRotation(input.GetAxis(InputAxis::XAxis) * rotateSpeed * InDeltaSeconds);
transform.AddPosition(transform.GetLocalY() * input.GetAxis(InputAxis::YAxis) * moveSpeed * InDeltaSeconds);
}
// 4. 렌더링 로직 단계
// 렌더링 로직을 담당하는 함수
void SoftRenderer::Render2D()
{
// 렌더링 로직에서 사용하는 모듈 내 주요 레퍼런스
auto& r = GetRenderer();
const auto& g = Get2DGameEngine();
// 배경에 격자 그리기
DrawGizmo2D();
// 렌더링 로직의 로컬 변수
size_t totalObjectCount = g.GetScene().size();
// 씬을 구성하는 모든 게임 오브젝트의 순회
for (auto it = g.SceneBegin(); it != g.SceneEnd(); ++it)
{
// 게임 오브젝트의 레퍼런스를 얻기
const GameObject& gameObject = *(*it);
if (!gameObject.HasMesh() || !gameObject.IsVisible())
{
continue;
}
// 렌더링에 필요한 게임 오브젝트의 주요 레퍼런스를 얻기
const Mesh& mesh = g.GetMesh(gameObject.GetMeshKey());
const TransformComponent& transform = gameObject.GetTransform();
Matrix3x3 finalMatrix = transform.GetModelingMatrix();
// 게임 오브젝트의 렌더링 수행 - 다음 절의 렌더링 파이프라인의 시작.
DrawMesh2D(mesh, finalMatrix, gameObject.GetColor());
// 플레이어의 정보를 화면에 출력
if (gameObject == PlayerGo)
{
r.PushStatisticText("Player Position : " + transform.GetPosition().ToString());
r.PushStatisticText("Player Rotation : " + std::to_string(transform.GetRotation()) + " (deg)");
r.PushStatisticText("Player Scale : " + std::to_string(transform.GetScale().X));
}
}
}
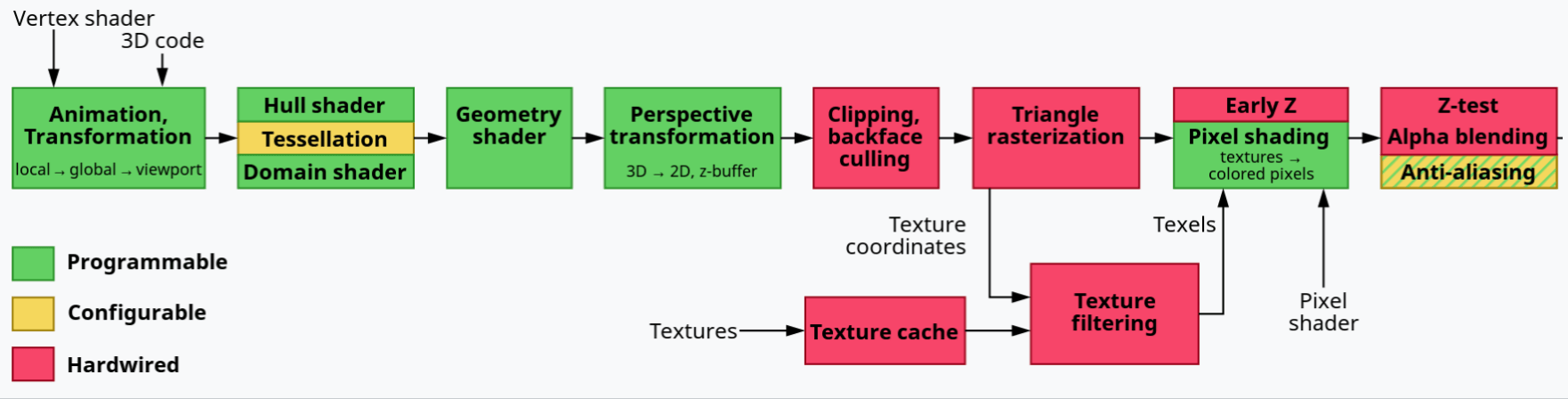
렌더링 파이프라인 #
- 렌더링 파이프라인(Rendering pipeline)
- 게임 제작의 렌더링은 GPU가 처리한다. GPU 내부에 설정된 렌더링 워크플로우를 렌더링 파이프라인이라고 한다.
- 드로우 콜(Drawcall)
- CPU가 GPU에게 렌더링 작업을 수행하도록 명령을 하는 것이다.
- (저자가 제작한 게임 엔진에서는)
DrawMesh2D()를 호출하는 것이 드로우 콜이라고 할 수 있겠다.
- (저자가 제작한) 렌더링 파이프라인
| 순서 | 단계 | 설명 |
|---|---|---|
| 1 | 정점 변환과 처리 단계 | 메시에 설정된 정점의 데이터는 로컬 공간을 기준으로 설정되어 있다. 이것을 월드 공간 중심으로 변환하여 화면에 그려질 정점의 최종 위치 값을 구한다. 즉, 로컬 공간의 좌표에 모델링 행렬을 곱한다. DrawMesh2D(), VertexShader2D() |
| 2 | 픽셀화와 픽셀 처리 단계 |
Chapter 8에서 보았던 무게중심좌표를 활용해서 삼각형 영역의 픽셀을 추려내고, 색상을 결정한다. 해당 픽셀의 UV에 대응되는 색상을 가져온 후 필요하다면 추가로 조명 효과 등을 적용해서 최종 픽셀 색상을 설정한다. DrawTriangle2D(), FragmentShader2D() |
// 1. 정점 변환과 처리
// 메시를 그리는 함수
void SoftRenderer::DrawMesh2D(const class DD::Mesh& InMesh, const Matrix3x3& InMatrix, const LinearColor& InColor)
{
// 메시의 구조를 파악하기 위한 로컬 변수
size_t vertexCount = InMesh.GetVertices().size();
size_t indexCount = InMesh.GetIndices().size();
size_t triangleCount = indexCount / 3;
// 메시 정보를 렌더러가 사용할 정점 버퍼와 인덱스 버퍼로 변환
std::vector<Vertex2D> vertices(vertexCount);
std::vector<size_t> indice(InMesh.GetIndices());
for (size_t vi = 0; vi < vertexCount; ++vi)
{
vertices[vi].Position = InMesh.GetVertices()[vi];
if (InMesh.HasColor())
{
vertices[vi].Color = InMesh.GetColors()[vi];
}
if (InMesh.HasUV())
{
vertices[vi].UV = InMesh.GetUVs()[vi];
}
}
// 정점 변환 진행!!
VertexShader2D(vertices, InMatrix);
// 그리기모드 설정
FillMode fm = FillMode::None;
if (InMesh.HasColor())
{
fm |= FillMode::Color;
}
if (InMesh.HasUV())
{
fm |= FillMode::Texture;
}
// 메시를 삼각형으로 쪼개서 각각 그리기
for (int ti = 0; ti < triangleCount; ++ti)
{
int bi0 = ti * 3, bi1 = ti * 3 + 1, bi2 = ti * 3 + 2;
std::vector<Vertex2D> tvs = { vertices[indice[bi0]] , vertices[indice[bi1]] , vertices[indice[bi2]] };
// 2. 픽셀화
DrawTriangle2D(tvs, InColor, fm);
}
}
- 셰이더(Shader)
- GPU의 렌더링 파이프라인의 몇몇 부분은 프로그래밍이 가능하다. 이런 부분을 개발자가 프로그래밍해서 만들어낸, 렌더링 효과를 계산하는 함수를 셰이더라고 한다.
- 정점 셰이더(Vertex Shader)
- 개발자들이 변환을 직접 설계해서 만든 정점 처리 함수이다.
// 정점 셰이더
FORCEINLINE void VertexShader2D(std::vector<Vertex2D>& InVertices, const Matrix3x3& InMatrix)
{
// 위치 값에 최종 행렬을 적용해 변환
for (Vertex2D& v : InVertices)
{
v.Position = InMatrix * v.Position;
}
}
// 2. 픽셀화와 픽셀 처리
// 삼각형을 그리는 함수
void SoftRenderer::DrawTriangle2D(std::vector<DD::Vertex2D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
// 렌더링 로직에서 사용하는 모듈 내 주요 레퍼런스
auto& r = GetRenderer();
const GameEngine& g = Get2DGameEngine();
const Texture& texture = g.GetTexture(GameEngine::BaseTexture);
if (IsWireframeDrawing())
{
// 와이어 프레임 모드
}
else
{
// ... 삼각형 칠하기
// 삼각형 영역 내 모든 점을 점검하고 색칠
for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
{
for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
{
ScreenPoint fragment = ScreenPoint(x, y);
Vector2 pointToTest = fragment.ToCartesianCoordinate(_ScreenSize);
Vector2 w = pointToTest - InVertices[0].Position;
float wdotu = w.Dot(u);
float wdotv = w.Dot(v);
float s = (wdotv * udotv - wdotu * vdotv) * invDenominator;
float t = (wdotu * udotv - wdotv * udotu) * invDenominator;
float oneMinusST = 1.f - s - t;
if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
{
Vector2 targetUV = InVertices[0].UV * oneMinusST + InVertices[1].UV * s + InVertices[2].UV * t;
// 색상 결정 진행!!
r.DrawPoint(fragment, FragmentShader2D(texture.GetSample(targetUV), LinearColor::White));
}
}
}
}
}
- 파편(Fragment)
- GPU에서는 삼각형을 구성하는 픽셀을 파편이라고 한다.
- 파편 셰이더(Fragment Shader) 혹은 픽셀 셰이더(Pixel Shader)
- 개발자들이 직접 설계한, 최종 픽셀을 계산하는 함수이다.
// 픽셀 셰이더 (단순하게 흰색을 합성해서 고유의 색을 표현하도록 함)
FORCEINLINE LinearColor FragmentShader2D(LinearColor& InColor, const LinearColor& InColorParam)
{
return InColor * InColorParam;
}
카메라 시스템 #
- 게임 엔진에는 개발자 관점에서 바라보는 게임 공간과 게이머가 바라보는 게임 공간, 이 두 가지 화면을 제공한다.
- 그렇다면 게이머를 위한 카메라는 월드 공간에 어떻게 설정할 수 있을까?
가상 공간의 카메라 #
- 뷰포트(Viewport)
- 카메라는 자신이 출력할 화면의 해상도 정보를 가지고 월드의 일부를 그려낸다. 이 때 카메라가 출력할 화면의 크기 정보를 뷰포트라고 한다.
- 즉, 게이머가 보는 게임 공간의 크기가 바로 뷰포트다.
- 뷰 공간(View space)
- 카메라에 설정된 뷰포트 정보를 바탕으로 월드 공간의 일부분을 렌더링해야 한다. 이를 위해서는 카메라를 중심으로 물체의 트랜스폼을 재조정하는 작업이 필요하다.
- 여기서 카메라를 중심으로 변환한 공간을 뷰 공간이라고 한다.
- 로컬 공간, 월드 공간, 뷰 공간의 개념을 정리하면 다음과 같다.
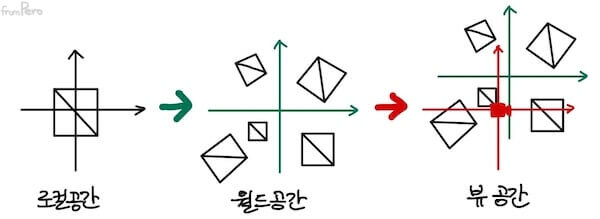
- 카메라를 중심으로 전개되는 뷰 공간을 어떻게 설계할 수 있을까?
- 예를 들어, 월드 공간에 카메라가 $(-10, -10)$에 있고, 어떤 물체가 $(10, 10)$에 있다고 하자. 그렇다면 카메라로부터 해당 게임 오브젝트의 상대적 위치는 $(20, 20)$이 된다.
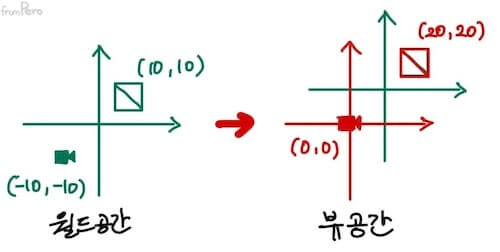
- 어떻게 하면 그 물체의 월드 공간 좌표인 $(10, 10)$을 뷰 공간 좌표인 $(20, 20)$로 바꿀 수 있을까?
- 뷰 행렬(View matrix)
- 모델링 행렬이 로컬 공간의 좌표를 월드 공간의 좌표로 변환해준다면, 뷰 행렬은 월드 공간의 좌표를 뷰 공간의 좌표로 변환해준다.
- 위 그림을 보면, 뷰 공간 좌표인 $(20, 20)$은 물체의 월드 공간 좌표에다가 카메라의 위치를 기준으로 측정한 월드 원점의 상대 좌표인 $(10, 10)$을 더하면 얻을 수 있다.
- 그리고 그 상대 좌표는 카메라의 월드 공간 좌표를 반전시켜서 얻을 수 있다. 즉, 이동 행렬의 역행렬을 사용해서 계산하면 된다.
$$V = \begin{bmatrix} 1 & 0 & -t_x \\ 0 & 1 & -t_y \\ 0 & 0 & 1 \end{bmatrix}$$
- 따라서, 로컬 공간 $v_{local}$을 뷰 공간 $v_{view}$으로 변환하는 과정은 다음과 같다.
- $v_{view} = V \cdot M \cdot v_{local}$
- 즉, 행렬 $VM$은 로컬 공간을 뷰 공간으로 변환한다.
- 다음은 플레이어를 따라가는 카메라의 로직을 구현한 예제이다.
// 게임 로직을 담당하는 함수
void SoftRenderer::Update2D(float InDeltaSeconds)
{
// 게임 로직에서 사용하는 모듈 내 주요 레퍼런스
auto& g = Get2DGameEngine();
const InputManager& input = g.GetInputManager();
// 게임 로직의 로컬 변수
static float moveSpeed = 200.f;
static float rotateSpeed = 180.f;
static float scaleMin = 15.f;
static float scaleMax = 30.f;
static float scaleSpeed = 180.f;
static float minDistance = 1.f; // 플레이어와 카메라의 위치가 일치할 최소거리
static float lerpSpeed = 2.f; // 플레이어가 카메라를 쫒아가는 속도
// 플레이어에 대한 주요 레퍼런스
GameObject& goPlayer = g.GetGameObject(PlayerGo);
TransformComponent& transform = goPlayer.GetTransform();
// 입력에 따른 플레이어 위치와 크기의 변경
transform.AddPosition(Vector2(input.GetAxis(InputAxis::XAxis), input.GetAxis(InputAxis::YAxis)).GetNormalize() * moveSpeed * InDeltaSeconds);
float newScale = Math::Clamp(transform.GetScale().X + scaleSpeed * input.GetAxis(InputAxis::ZAxis) * InDeltaSeconds, scaleMin, scaleMax);
transform.SetScale(Vector2::One * newScale);
transform.AddRotation(input.GetAxis(InputAxis::WAxis) * rotateSpeed * InDeltaSeconds);
// 플레이어를 따라다니는 카메라의 트랜스폼
TransformComponent& cameraTransform = g.GetMainCamera().GetTransform();
Vector2 playerPos = transform.GetPosition();
Vector2 cameraPos = cameraTransform.GetPosition();
if ((playerPos - cameraPos).SizeSquared() < minDistance * minDistance)
{
// 최소거리보다 작으면 플레이어 위치로 간다.
cameraTransform.SetPosition(playerPos);
}
else // 최소거리보다 크면 서서히 이동한다.
{
float ratio = Math::Clamp(lerpSpeed * InDeltaSeconds, 0.f, 1.f);
Vector2 newCameraPos = cameraPos + (playerPos - cameraPos) * ratio;
cameraTransform.SetPosition(newCameraPos);
}
}
// 렌더링 로직을 담당하는 함수
void SoftRenderer::Render2D()
{
// 렌더링 로직에서 사용하는 모듈 내 주요 레퍼런스
auto& r = GetRenderer();
const auto& g = Get2DGameEngine();
const auto& texture = g.GetTexture(GameEngine::BaseTexture);
// 배경에 격자 그리기
DrawGizmo2D();
// 렌더링 로직의 로컬 변수
size_t totalObjectCount = g.GetScene().size();
Matrix3x3 viewMatrix = g.GetMainCamera().GetViewMatrix(); // 뷰 행렬
// 씬을 구성하는 모든 게임 오브젝트의 순회
for (auto it = g.SceneBegin(); it != g.SceneEnd(); ++it)
{
// 게임 오브젝트의 레퍼런스를 얻기
const GameObject& gameObject = *(*it);
if (!gameObject.HasMesh() || !gameObject.IsVisible())
{
continue;
}
// 렌더링에 필요한 게임 오브젝트의 주요 레퍼런스를 얻기
const Mesh& mesh = g.GetMesh(gameObject.GetMeshKey());
const TransformComponent& transform = gameObject.GetTransform();
Matrix3x3 finalMatrix = viewMatrix * transform.GetModelingMatrix(); // 뷰행렬 * 모델링 행렬으로 VM을 구한다
// 게임 오브젝트의 렌더링 수행
DrawMesh2D(mesh, finalMatrix, gameObject.GetColor());
// 플레이어의 정보를 화면에 출력
if (gameObject == PlayerGo)
{
r.PushStatisticText("Player Position : " + transform.GetPosition().ToString());
r.PushStatisticText("Player Rotation : " + std::to_string(transform.GetRotation()) + " (deg)");
r.PushStatisticText("Player Scale : " + std::to_string(transform.GetScale().X));
}
}
}