[Game Math] Chapter 8. 삼각형: 물체를 구성하는 가장 작은 단위

세 점의 결합 #

• Chapter 6에서 보았듯이, 아핀 결합은 여러개의 점을 결합해서 새로운 점을 생성하는 수식이다. 이 때 스칼라 값들은 그 합이 모두 $1$이어야 했다.
• 세 점 $P_1$, $P_2$, $P_3$를 결합하는 경우에도 스칼라값 3개의 합은 $1$이 되어야 할 것이다.

$$P’ = s \cdot P_1 + t \cdot P_2 + (1 - s - t) \cdot P_3$$ $$(P’ - P_3) = s(P_1 - P_3) + t(P_2 - P_3)$$ $$\vec{w} = s \cdot \vec{u} + t \cdot \vec{v}$$

• 이 때 벡터 $\vec{u}$와 $\vec{v}$가 선형 독립의 관계라면, 벡터 $\vec{w}$는 2차원 벡터 공간 $\mathbb{R}^2$에 존재하는 모든 벡터가 될 수 있다. 즉, 세 점의 아핀 결합은 평면의 모든 점을 만들어낸다.

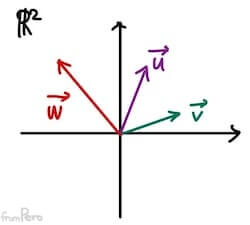
• 여기서 $s$와 $t$의 값의 범위를 $[0, 1]$로 고정시키면 어떻게 될까?
  • 해당 영역은 삼각형이 된다.

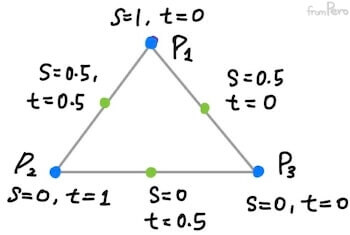
• 컨벡스 결합(Convex combination)
  • 아핀 결합에서 모든 스칼라 값을 $[0, 1]$ 범위로 한정한 결합
• 컨벡스 결합은 Chapter 6의 아핀 결합식에 각 스칼라 범위를 $[0, 1]$로 제한하는 조건을 추가해서 다음과 같이 표현할 수 있다.

$$\displaystyle\sum_{i=1}^{n} c_i \cdot P_i (s.t. \displaystyle\sum_{i=1}^{n} c_i = 1, 0 \leq c_i \leq 1)$$

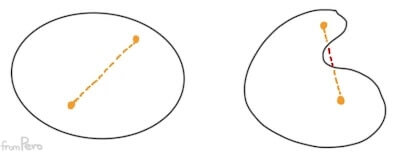
• 컨벡스 영역(Convex region) - 왼쪽 그림
  • 선분이나 삼각형처럼 컨벡스 결합으로 만든 영역.
  • 컨벡스는 사전적으로 ‘볼록한’을 뜻한다.
  • 수학에서 정의하는 볼록함이란, 영역 내 임의의 두 점을 연결한 선분을 만들었을 때 그 선분은 언제나 해당 컨벡스 영역 안에 속하는 성질을 의미한다.
• 컨케이브 영역(Concave region) - 오른쪽 그림
  • 컨벡스 영역과 반대로, 임의의 두 점을 연결한 선분이 영역 밖으로 벗어나는 경우가 있는 영역이다.

• 4개의 점을 결합하는 컨벡스 결합은 어떻게 구성될까? $$\vec{x} = a \cdot \vec{u} + b \cdot \vec{v} + c \cdot \vec{w}$$
  • 세 벡터 $\vec{u}$, $\vec{v}$, $\vec{w}$가 선형 독립 관계를 이룬다면 3차원 공간의 모든 벡터를 생성할 수 있으므로, 벡터 $\vec{x}$는 3차원 공간의 벡터가 된다.
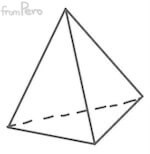
  • 여기서 스칼라 값을 $[0, 1]$ 범위로 제한한다면 삼각뿔(Tetrahedron) 영역이 형성된다.
  • 이 또한 컨벡스 성질을 가진다.

메시 #

• 메시(Mesh)
  • 삼각형을 중심으로 물체에 관련된 정보를 기록한 데이터이다.
  • 메시는 다수의 삼각형으로 구성되고, 삼각형은 세 개의 점으로 구성되므로, 메시는 결국 다수의 점으로 구성된다고 볼 수 있다.
• 정점(Vertex)
  • 메시는 삼각형으로 물체의 외형을 표현하므로 삼각형의 위치정보를 가지고 있어야 한다. 이에 추가로 위치 뿐만 아니라 색상, 방향과 같은 부가 정보도 함께 제공한다. 이렇게 위치 정보와 부가 정보를 묶은 특별한 점을 정점이라고 한다.
  • 즉, 메시는 정점들이 모인 데이터라고 할 수 있다.

• 와이어 프레임(Wireframe)
  • 삼각형의 외곽선만 그려 메시를 표현하는 방법을 와이어 프레임이라고 한다.

• 정점 버퍼(Vertex buffer)
  • 메시의 정점 정보를 빠르게 읽기 위해서 메모리에 정점 정보를 일렬로 나열하는 배열의 형태로 관리한다. 이것을 정점 버퍼라고 한다.
• 인덱스 버퍼(Index buffer)
  • 정점 정보만으로는 삼각형을 만들 수 없으므로, 삼각형을 구성하는 정점의 인덱스(순번)만 기록한 배열을 별도로 만들어서 관리한다. 이것을 인덱스 버퍼라고 한다.
  • 인덱스 버퍼는 삼각형의 수만큼 필요하기 때문에 인덱스 버퍼의 크기는 항상 3의 배수이다.

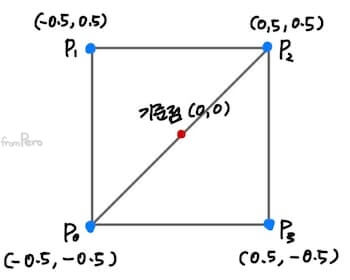
• 다음은 정사각형의 와이어 프레임을 그리는 예제이다.
  • 정사각형을 구성하는 메시 정보를 표현하면 다음과 같다.
  • 여기서 정점 0, 2번은 두 삼각형이 공유해 사용할 수 있다.

• 정점 버퍼

  순서	좌표
  0	(-0.5, -0.5)
  1	(-0.5, 0.5)
  2	(0.5, 0.5)
  3	(0.5, -0.5)

• 인덱스 버퍼

  순서	삼각형	정점 순서
  0	0	0
  1	0	1
  2	0	2
  3	1	0
  4	1	2
  5	1	3

// 정점 배열
static constexpr std::array<Vertex2D, vertexCount> rawVertices = {
    Vertex2D(Vector2(-sqareHalfSize, -squareHalfSize)),
    Vertex2D(Vector2(-sqareHalfSize, squareHalfSize)),
    Vertex2D(Vector2(sqareHalfSize, squareHalfSize)),
    Vertex2D(Vector2(sqareHalfSize, -squareHalfSize))
};

// 인덱스 배열
static constexpr std::array<size_t, triangleCount * 3> indices = {
    0, 1, 2,
    0, 2, 3
};

// ... 아핀 변환행렬을 곱해서 최종 행렬 finalMatrix를 생성한다. 

// 최종 행렬을 곱해서 위치 지정
static std::vector<Vertex2D> vertices(vertexCount);
for (size_t vi = 0; vi < vertexCount; ++vi)
{
    vertices[vi].Position = finalMatrix * rawVertices[vi].Position;
}

// 정점 배열과 인덱스 배열을 사용해서 삼각형의 점을 서로 이어준다. 
for (size_t ti = 0; ti < triangleCount; ++i)
{
    size_t bi = ti * 3;
    r.DrawLine(vertices[indices[bi]].Position, vertices[indices[bi + 1]].Position, _WireframeColor);
    r.DrawLine(vertices[indices[bi]].Position, vertices[indices[bi + 2]].Position, _WireframeColor);
    r.DrawLine(vertices[indices[bi + 1]].Position, vertices[indices[bi + 2]].Position, _WireframeColor);    
}

무게중심좌표 #

• 세 점의 아핀 결합 수식에서

$$P’ = s \cdot P_1 + t \cdot P_2 + (1 - s - t) \cdot P_3$$

• 스칼라 값 $s$, $t$, $1 - s - t$는 모두 실수이다. 이들을 묶어서 하나의 3차원 벡터로 생성할 수 있겠다.

$$(s, t, 1 - s - t)$$

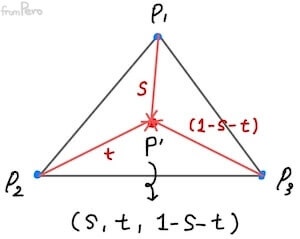
• 이렇게 아핀 결합의 스칼라를 묶어서 만든 좌표를 무게중심좌표(Barycentric coordinate)라고 한다.

아핀 결합으로 생성된 점이 삼각형 내부에 있는지 판별 #

• 이전에 보았듯이 아핀 결합이 삼각형이 되려면 스칼라 값 $s$, $t$, $1 - s - t$는 $[0, 1]$ 범위 내에 있어야 한다.
  • 따라서 $[0, 1]$ 외부에 있다면 아핀 결합으로 생성된 점이 삼각형 외부에 있다고 볼 수 있다.

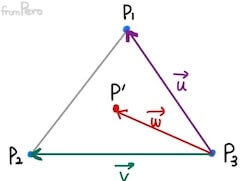
• 이전에 보았던 $\vec{w} = s \cdot \vec{u} + t \cdot \vec{v}$ 이 수식에 벡터 $\vec{u}$와 $\vec{v}$를 내적해보자.

$$\vec{w} \cdot \vec{u} = ( s \cdot \vec{u} + t \cdot \vec{v}) \cdot \vec{u}$$ $$\vec{w} \cdot \vec{v} = ( s \cdot \vec{u} + t \cdot \vec{v}) \cdot \vec{v}$$

• 이것을 분배법칙에 따라 풀어준다.

$$\vec{w} \cdot \vec{u} = s(\vec{u} \cdot \vec{u}) + t (\vec{u} \cdot \vec{v})$$ $$\vec{w} \cdot \vec{v} = s(\vec{u} \cdot \vec{v}) + t (\vec{v} \cdot \vec{v})$$

• 위의 식에는 $(\vec{u} \cdot \vec{v})$를, 및에 식에는 $(\vec{u} \cdot \vec{u})$를 곱해 각각 전개해보자.

$$(\vec{w} \cdot \vec{u})(\vec{u} \cdot \vec{v}) = s(\vec{u} \cdot \vec{u})(\vec{u} \cdot \vec{v}) + t(\vec{u} \cdot \vec{v})(\vec{u} \cdot \vec{v})$$ $$(\vec{w} \cdot \vec{v})(\vec{u} \cdot \vec{u}) = s(\vec{u} \cdot \vec{v})(\vec{u} \cdot \vec{u}) + t(\vec{v} \cdot \vec{v})(\vec{u} \cdot \vec{u})$$

• 위에 식에서 아래식을 빼 $s$를 소거하고 $t$만 남긴다.

$$ t = \frac{ (\vec{w} \cdot \vec{u})(\vec{u} \cdot \vec{v}) - (\vec{w} \cdot \vec{v})(\vec{u} \cdot \vec{u}) }{ (\vec{u} \cdot \vec{v})^2 - (\vec{u} \cdot \vec{u})(\vec{v} \cdot \vec{v}) }$$

• 예전 식에서 이번에는 위의 식에 $(\vec{v} \cdot \vec{v})$를, 및에 식에는 $(\vec{u} \cdot \vec{v})$를 곱해 각각 전개해보자.

$$(\vec{w} \cdot \vec{u})(\vec{v} \cdot \vec{v}) = s(\vec{u} \cdot \vec{u})(\vec{v} \cdot \vec{v}) + t(\vec{u} \cdot \vec{v})(\vec{v} \cdot \vec{v})$$ $$(\vec{w} \cdot \vec{v})(\vec{u} \cdot \vec{v}) = s(\vec{u} \cdot \vec{v})(\vec{u} \cdot \vec{v}) + t(\vec{v} \cdot \vec{v})(\vec{u} \cdot \vec{v})$$

• 위의 식에서 아래 식을 빼 $t$를 소거하고 $s$만 남긴다.

$$ s = \frac{ (\vec{w} \cdot \vec{v})(\vec{u} \cdot \vec{v}) - (\vec{w} \cdot \vec{u})(\vec{v} \cdot \vec{v}) }{ (\vec{u} \cdot \vec{v})^2 - (\vec{u} \cdot \vec{u})(\vec{v} \cdot \vec{v}) }$$

• 이렇게 얻어진 무게중심좌표 $(s, t, 1-s-t)$의 세 값 모두 $[0, 1]$ 범위 내에 있다면 새로 생성된 점은 삼각형 안에 있다고 할 수 있다. 반대로 그 범위를 벗어난다면, 삼각형 밖에 있다고 판단할 수 있다.
• 공통분모 $(\vec{u} \cdot \vec{v})^2 - (\vec{u} \cdot \vec{u})(\vec{v} \cdot \vec{v})$의 결과가 $0$이 나올 수도 있으므로 주의해야한다. 분모 값이 $0$이면 무게중심좌표를 구할 수가 없다.
  • 공통분모에서 내적을 $\cos$공식으로 변경하면 다음과 같아진다. $$(|\vec{u}||\vec{v}|)^2 \cdot \cos^2\theta - (|\vec{u}||\vec{v}|)^2$$
  • 이 값이 $0$이 되기 위한 조건은 $\vec{u}$ 혹은 $\vec{v}$의 크기가 $0$이거나, 그 두 벡터가 이루는 각 $\theta$가 $0^{\circ}$ 혹은 $180^{\circ}$일 때다. 이것은 두 벡터가 평행함을 의미한다.
  • 두 벡터가 평행하면 선형 종속의 관계를 가지며 삼각형이 아니라 선분을 만들어낸다. 이런 삼각형을 퇴화삼각형(Degenerate triangle) 이라고 하며, 퇴화삼각형은 그리기에서 제외한다.

• 다음은 무게중심좌표를 사용해서 정사각형을 칠하는 예제이다.

// ... 이전 예제와 똑같은 과정을 거친다. 

for (size_t ti = 0; ti < triangleCount; ++i)
{
    size_t bi = ti * 3;
    
    // 삼각형의 세 점
    std::array<Vertex2D, 3> tv = {vertices[indices[bi]], vertices[indices[bi + 1]], vertices[indices[bi + 2]]};

    // ... 삼각형의 세 점을 통해 minX, minY, maxX, maxY를 구한다. 

    // u벡터와 v벡터
    Vector2 u = tv[1].Position - tv[0].Position;
    Vector2 v = tv[2].Position - tv[0].Position;

    // 공통분모 구하기
    float uDotv = u.Dot(v);
    float vDotv = v.Dot(v);
    float uDotu = u.Dot(u);
    float denominator = uDotv * uDotv - vDotv * uDotu;

    // 퇴화삼각형은 그리지 않는다!!
    if (denominator == 0.0f) continue;

    float invDenominator = 1.f / denominator;

    // ... minX, minY, maxX, maxY를 스크린 좌표계로 옮기고, 화면을 넘어서면 클리핑한다. 

    // 삼각형을 둘러싸는 사각형 영역의 픽셀을 모두 순회한다. 
    for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
    {
        for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++x))
        {
            // 스크린 좌표계와 데카르트 좌표계
            ScreenPoint fragment = ScreenPoint(x, y);
            Vector2 pointToTest = fragment.ToCartesianCoordinate(_ScreenSize);
        
            // w벡터
            Vector2 w = pointToTest - tv[0].Position;
            float wDotu = w.Dot(u);
            float wDotv = w.Dot(v);
        
            // s, t, 1-s-t 구하기
            float s = (wDotv * uDotv - wDotu * vDotv) * invDenominator;
            float t = (wDotu * uDotv - wDotv * uDotu) * invDenominator;
            float oneMinusST = 1.f - s - t;
        
            // 컨벡스 조건을 만족할 때만 점 찍기!!
            if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) &&((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
            {
                r.DrawPoint(fragment, LinearColor::Blue);
            }
        }
    }
}

픽셀이 삼각형의 세 점으로부터 얼마나 영향을 받는지 파악 #

• 무게중심좌표의 값은 주어진 픽셀이 삼각형의 세 점으로부터 얼마나 영향을 받는지 파악하는 용도로도 활용할 수 있다.
  • 예를 들어 어떤점의 무게중심좌표가 $(0.333, 0.333, 0.333)$이라면 삼각형의 세 점이 균일하게 영향을 미치는 삼각형의 무게중심에 그 점이 위치한다고 볼 수 있다.

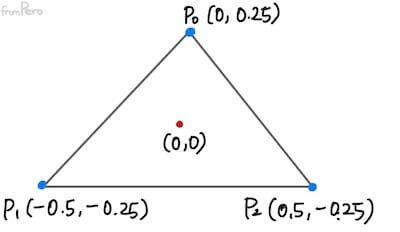
• 다음은 무게중심좌표를 사용해서 삼각형에 색상을 입히는 예제이다.

• 정점 버퍼

  인덱스	좌표	색상(RGB)
  0	(0, 0.25)	(1, 0, 0) Red
  1	(-0.5, -0.25)	(0, 1, 0) Green
  2	(0.5, -0.25)	(0, 0, 1) Blue

• 인덱스 버퍼

  순서	삼각형	정점 순서
  0	0	0
  1	0	2
  2	0	1

// 정점 배열에 색상정보도 추가한다. 
std::array<Vertex2D, vertexCount> rawVertices = {
    Vertex2D(Vector2(0.f, 0.25f), LinearColor(1.f, 0.f, 0.f)), 
    Vertex2D(Vector2(-0.5f, -0.25f), LinearColor(0.f, 1.f, 0.f)),
    Vertex2D(Vector2(0.5f, -0.25f), LinearColor(0.f, 0.f, 1.f))    
};

// 인덱스 배열
static constexpr std::array<size_t, triangleCount * 3> indices = {
    0, 2, 1
};

// ... 아핀 변환행렬을 곱해서 최종 행렬 finalMatrix를 생성한다. 

// 최종 행렬을 곱해서 위치 지정. 색상 정보도 함께 복사한다. 
static std::vector<Vertex2D> vertices(vertexCount);
for (size_t vi = 0; vi < vertexCount; ++vi)
{
    vertices[vi].Position = finalMatrix * rawVertices[vi].Position;
    vertices[vi].Color = rawVertices[vi].Color;
}

for (size_t ti = 0; ti < triangleCount; ++i)
{
    // ...

    for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
    {
        for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++x))
        {
            // ...
                
            // 무게중심좌표와 정점의 색상정보를 선형 보간해서 최종 픽셀 색상값을 계산한다. 
            if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) &&((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
            {
                LinearColor outColor = tv[0].Color * oneMinusST + tv[1].Color * s + tv[2].Color * t;
                
                r.DrawPoint(fragment, outColor);
            }
        }
    }
}

텍스처 매핑 #

• 무게중심좌표는 메시에 이미지를 입하는 용도로도 활용할 수 있다.
• 텍스처(Texture)
  • 메시에 이미지를 입히기 위해 변환된 데이터이다.
• 텍스처 매핑(Texture mapping)
  • 메시에 이미지를 입하는 작업이다.
• UV 좌표계
  • 사진이나 그림을 저장한 이미지는 각기 고유한 해상도를 가진다. 메시에 이것을 입히기 위해서 텍스처로 변환하면 관리 방식을 통일하기 위해 이미지 고유의 해상도에 관계없이 가로, 세로 크기가 $1$로 정규화된다.
  • 이처럼 렌더링 과정에서 텍스처를 사용할 때는 $[0, 1]$범위로 구성된 2차원 좌표계를 사용하는 데 이 좌표계를 UV좌표계라고 한다.
  • U는 가로정보, V는 세로정보를 나타낸다.
• 예를 들어, 왼쪽 하단을 원점으로 잡고 우상단으로 증가하는 방식의 UV좌표계는 다음과 같을 것이다.

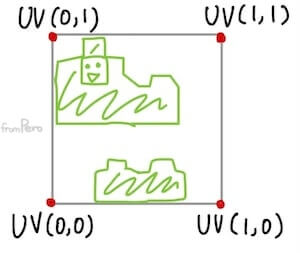
• 텍스처 매핑 방법
  • 삼각형의 세 정점에 UV 좌표 정보를 추가한다. 그리고 삼각형을 구성하는 각 픽셀들의 무게중심좌표를 계산해서 UV좌표와 선형보간한다. 이렇게 하면 해당 픽셀에 해당하는 UV값을 얻어낼 수 있다.
  • 이 UV값에 대응하는 텍스처의 색상 정보를 얻은 후에 이것을 최정 픽셀의 색상으로 지정하면 텍스처 매핑이 완성된다.

• 다음은 무게중심좌표와 UV좌표를 사용해서 정사각형에 얼굴 텍스처를 입히는 예제이다.

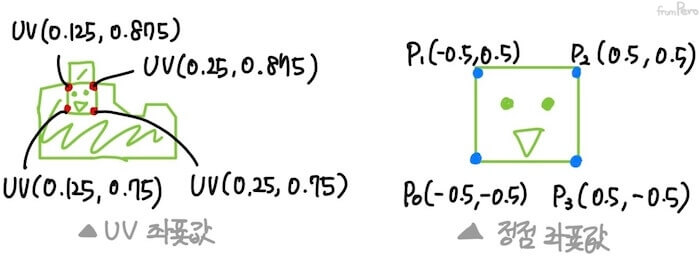
• 정점 버퍼

  인덱스	좌표	UV좌표
  0	(-0.5, -0.5)	(0.125, 0.75)
  1	(-0.5, 0.5)	(0.125, 0.875)
  2	(0.5, 0.5)	(0.25, 0.75)
  3	(0.5, -0.5)	(0.25, 0.875)

• 인덱스 버퍼

  순서	삼각형	정점 순서
  0	0	0
  1	0	1
  2	0	2
  3	1	0
  4	1	2
  5	1	3

// 텍스쳐를 가져온다. 
const auto& texture = g.GetTexture(GameEngine::BaseTexture);

//...

// 정점 배열에 UV값도 추가한다. 
std::array<Vertex2D, vertexCount> rawVertices = {
    Vertex2D(Vector2(-sqareHalfSize, -squareHalfSize), LinearColor(), Vector2(0.125f, 0.75f)), 
    Vertex2D(Vector2(-sqareHalfSize, squareHalfSize), LinearColor(), Vector2(0.125f, 0.875f)), 
    Vertex2D(Vector2(sqareHalfSize, squareHalfSize), LinearColor(), Vector2(0.25f, 0.875f)), 
    Vertex2D(Vector2(sqareHalfSize, -squareHalfSize), LinearColor(), Vector2(0.25f, 0.75f)), 
};

// 인덱스 배열
static constexpr std::array<size_t, triangleCount * 3> indices = {
    0, 1, 2,
    0, 2, 3
};

// ... 아핀 변환행렬을 곱해서 최종 행렬 finalMatrix를 생성한다. 

// 최종 행렬을 곱해서 위치 지정. UV 정보도 함께 복사한다. 
static std::vector<Vertex2D> vertices(vertexCount);
for (size_t vi = 0; vi < vertexCount; ++vi)
{
    vertices[vi].Position = finalMatrix * rawVertices[vi].Position;
    vertices[vi].UV = rawVertices[vi].UV;
}

// 정점 배열과 인덱스 배열을 사용해서 삼각형의 점을 서로 이어준다.
for (size_t ti = 0; ti < triangleCount; ++i)
{
    // ...

    for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
    {
        for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++x))
        {
            // ...
        
            // 무게중심좌표와 정점의 UV좌표를 선형 보간해서 최종 UV값을 계산한다. 
            if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) &&((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
            {
                Vector2 targetUV = tv[0].UV * oneMinusST + tv[1].UV * s + tv[2].UV * t;
                
                r.DrawPoint(fragment, targetUV.GetSample(targetUV));
            }
        }
    }
}