[게임 수학] Chapter 7. 내적: 벡터 공간의 분석과 응용
Table of Contents
이득우의 게임 수학 책을 읽고 공부한 노트입니다.
벡터의 내적 #
- 내적(Dot product)
- 같은 차원의 두 벡터가 주어졌을 때, 벡터를 구성하는 각 성분을 곱한 후 이들을 더해 스칼라를 만들어내는 연산이다.
- $\vec{u} = (a, b)$, $\vec{v} = (c, d)$ 일 때,
$\vec{u} \cdot \vec{v} = a \cdot c + b \cdot d$
내적의 성질 #
- 교환법칙이 성립한다.
$$\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u}$$
- 결합법칙이 성립하지 않는다.
$$\vec{u} \cdot (\vec{v} \cdot \vec{w}) \neq (\vec{u} \cdot \vec{v}) \cdot \vec{w}$$
- 덧셈에 대한 분배법칙이 성립한다.
$$\vec{w} \cdot (\vec{u} + \vec{v}) = \vec{u} \cdot \vec{w} + \vec{v} \cdot \vec{w}$$
- 같은 벡터를 내적하면 크기를 제곱한 결과가 나온다.
$$\vec{v} \cdot \vec{v} = |\vec{v}|^2$$
- 두 벡터의 합의 내적은 두 벡터의 크기로 표현할 수 있다.
$$(\vec{u} + \vec{v}) \cdot (\vec{u} + \vec{v}) = |\vec{u}|^2 + |\vec{v}|^2 + 2(\vec{u} \cdot \vec{v})$$
내적과 삼각함수와의 관계 #
- 벡터의 내적은 두 벡터의 사잇각에 대한 $\cos$함수와 비례한다.
- $\vec{u} \cdot \vec{v} = |\vec{u}||\vec{v}|\cos\theta$
- 이 식을 유도해보자.
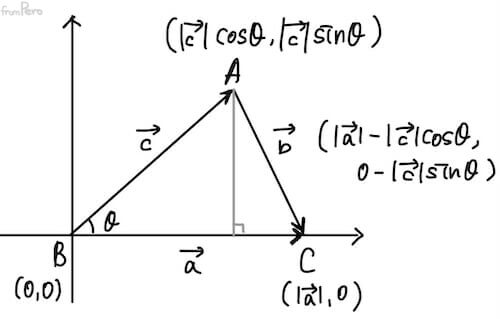
-
그림과 같이 구성되었을 때 벡터 $\vec{b}$의 크기를 제곱하면 다음과 같다. $$|\vec{b}|^2 = (|\vec{a}| - |\vec{c}|\cos\theta)^2 + |\vec{c}|^2\sin^2\theta$$ $$ = |\vec{a}|^2 - 2 |\vec{a}||\vec{c}|\cos\theta + |\vec{c}|^2\cos^2\theta + |\vec{c}|^2\sin^2\theta$$ $$ = |\vec{a}|^2 + |\vec{c}|^2 - 2 |\vec{a}||\vec{c}|\cos\theta$$
-
같은 벡터를 내적하면 벡터 크기의 제곱이 된다. $$|\vec{b}|^2 = \vec{b} \cdot \vec{b}$$ $$ = (\vec{a} + (-\vec{c})) \cdot (\vec{a} + (-\vec{c}))$$ $$ = |\vec{a}|^2 + |\vec{c}|^2 - 2\vec{a} \cdot \vec{c}$$
-
따라서 다음 식이 성립한다. $$\vec{a} \cdot \vec{c} = |\vec{a}||\vec{c}|\cos\theta$$
-
여기서 두 벡터의 크기가 $1$이면, 두 벡터의 내적은 $\cos$함수가 된다. $$\vec{u} \cdot \vec{v} = \cos\theta$$
- 두 벡터의 내적이 $0$이면, 두 벡터는 직교한다.
- 위의 공식에 따르면, 내적 값이 $0$이 되기 위한 조건은 $\cos$함수의 값이 $0$이 되는 경우 뿐이다.
- $\cos$함수의 값이 $0$이 되는 경우는 두 벡터의 사잇각이 $90^\circ$ 혹은 $270^\circ(-90^\circ)$인 경우다.
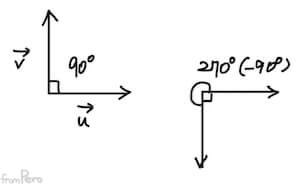
- 이것은 두 벡터가 서로 직교하는 경우이다.
- 벡터 공간에서 직교하는 두 표준기저벡터 $(0, 1)$, $(1, 0)$을 내적한 결과는 $0$이다. 그리고 이것을 $\theta$만큼 회전한 두 기저벡터 $(\cos\theta, \sin\theta)$, $(-\sin\theta, \cos\theta)$도 직교하기 때문에 내적한 결과는 똑같이 $0$이다.
행렬의 곱셈을 내적으로 표현하기 #
- 행렬과 벡터의 곱셈 연산을 내적으로 표현해보자.
$$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix}$$ $$ = \begin{bmatrix} (a, b) \cdot (x, y) \\ (c, d) \cdot (x, y) \end{bmatrix} $$
- 행렬과 행렬의 곱셈 연산을 내적으로 표현해보자.
$$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} e & f \\ g & h \end{bmatrix} = \begin{bmatrix} ae + bg & af + bh \\ ce + dg & cf + dh \end{bmatrix}$$ $$ = \begin{bmatrix} (a, b) \cdot (e, g) & (a, b) \cdot (f, h) \\ (c, d) \cdot (e, g) & (c, d) \cdot (f, h) \end{bmatrix} $$
- 직교 행렬(Orthogonal matrix)
- 정방행렬을 구성하는 모든 행벡터와 열벡터의 크기가 $1$이고, 벡터들이 서로 직교하는 행렬이다. $$Q = \begin{bmatrix} a & c \\ b & d \end{bmatrix}$$
- 위 행렬에서 $(a, c)$, $(b, d)$, $(a, b)$, $(c, d)$의 크기가 $1$이고, $(a, b)$와 $(c, d)$가 직교하면 직교 행렬이다.
- 직교행렬의 특징은 전치행렬이 곧 역행렬이라는 점이다. 따라서 직교행렬과 그 전치행렬의 곱은 항등행렬이된다.
- $Q \cdot Q^T = I$
- 이는 내적을 사용해서 증명할 수 있다.
- $(a, b)$와 $(c, d)$는 서로 직교하므로 두 벡터의 내적은 $0$이다. 그리고 행벡터와 열벡터의 크기가 $1$이므로 자기 자신과 내적한 결과는 $1$이 된다.
$$Q = \begin{bmatrix} a & c \\ b & d \end{bmatrix}$$ $$Q^T \cdot Q = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} a & c \\ b & d \end{bmatrix} $$ $$ = \begin{bmatrix} (a, b) \cdot (a, b) & (a, b) \cdot (c, d) \\ (c, d) \cdot (a, b) & (c, d) \cdot (c, d) \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I$$
- 회전 변환행렬은 직교행렬이다.
$$R_{\theta} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}$$ $$R_{\theta}^T \cdot R_{\theta} = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}$$ $$= \begin{bmatrix} \cos^2\theta + \sin^2\theta & 0 \\ 0 & \cos^2\theta + \sin^2\theta \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = I$$
- 강체 변환(Rigid Transformation)
- 물체의 형태가 그대로 유지되는 선형 변환이다.
- 조건
- 변화된 기저벡터의 크기는 모두 $1$이어야 한다.
- 모든 기저벡터는 서로 직교해야한다.
- 행렬식 값이 $1$이어야 한다.
- 회전 변환은 강체 변환이다.
- 회전 행렬은 앞서 보았듯이 직교 행렬이기 때문에 1, 2번 조건을 만족한다.
- 3번의 경우 행렬식 $ad - bc$가 다음과 같이 $1$이 된다.
$$det(R) = \cos^2\theta + \sin^2\theta = 1$$
(1) 앞뒤 판별 #
- 벡터의 크기 값은 언제나 양수이다. 따라서 내적의 부호는 $\cos$ 함수가 결정한다.
- $\cos$함수는 $(-90^\circ, 90^\circ)$에서 양의 부호를 가지고 $-90^\circ$와 $90^\circ$에서는 $0$이며, 나머지 범위에서는 음의 부호를 가진다.
- $\cos$함수는 $(-90^\circ, 90^\circ)$에서 양의 부호를 가지고 $-90^\circ$와 $90^\circ$에서는 $0$이며, 나머지 범위에서는 음의 부호를 가진다.
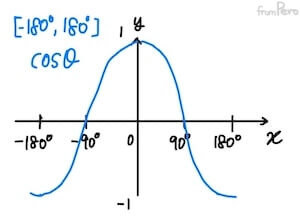
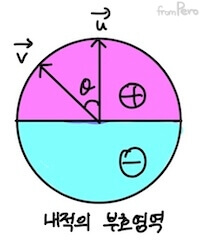
- 따라서 이를 응용하면 벡터 내적의 부호만 가지고도 다음과 같이 판단할 수 있다.
| 두 벡터 내적의 결과 | 의미 |
|---|---|
| 양수 | 두 벡터는 같은 방향을 향하고 있다. |
| 음수 | 두 벡터는 다른 방향을 향하고 있다. (서로 마주보고 있다.) |
| $0$ | 두 벡터는 직교한다. |
- 이것들을 응용해서 목표물이 캐릭터 앞에 있는지 뒤에 있는지를 판별할 수 있겠다.
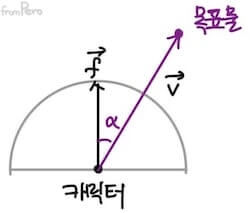
| $\vec{f} \cdot \vec{v}$의 결과 | 의미 |
|---|---|
| 양수 | 캐릭터 앞에 목표물이 있다. |
| 음수 | 캐릭터 뒤에 목표물이 있다. |
| $0$ | 캐릭터 바로 옆에 목표물이 있다. |
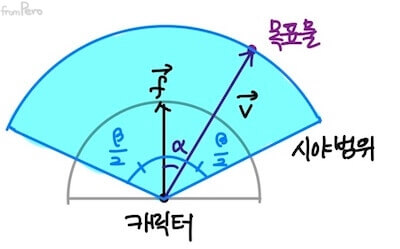
(2) 시야 판별 #
- 캐릭터에게 부여한 시야각이 $\beta$라고 하자. 그리고 캐릭터에서 목표물로 향하는 벡터 $\vec{v}$와의 사잇각을 $\alpha$라고 하자.
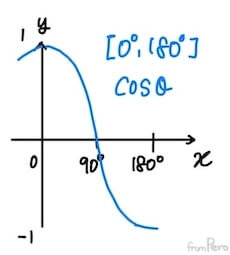
- $\cos$함수의 경우 $[0^\circ, 180^\circ]$에서는 각이 커질 수록 값이 작아진다.
-
이것을 활용해서 다음의 과정으로 캐릭터 시야 안에 목표물이 있는지 판별할 수 있다.
- (1) 시야각을 절반 나눈 각의 $\cos\frac{\beta}{2}$를 미리 계산해둔다.
- (2) 캐릭터 시선 벡터의 크기를 $1$로 정규화시킨 단위 벡터 $\hat{f}$을 구한다.
- (3) 캐릭터에서 목표물로 향하는 벡터를 정규화시킨 단위 벡터 $\hat{v}$을 구한다.
- (4) 그 두 벡터의 내적 결과는 $\hat{f} \cdot \hat{v} = \cos\alpha$가 된다. 이것을 앞서 계산해 두었던 $\cos\frac{\beta}{2}$와 비교한다.
-
이 때 $\hat{f} \cdot \hat{v}$가 $\cos\frac{\beta}{2}$보다 크다면 사잇각이 시야보다 작다는 것을 의미하므로 물체가 시야 영역에 들어왔음을 의미한다.
| 결과 | 의미 |
|---|---|
| $$\hat{f} \cdot \hat{v} \geq \cos\frac{\beta}{2}$$ | 목표물이 시야 범위 안에 있다. |
| $$\hat{f} \cdot \hat{v} \lt \cos\frac{\beta}{2}$$ | 목표물이 시야 범위 밖에 있다. |
- $atan2$함수를 사용해서 두 벡터가 이루는 각 $\alpha$를 구한 후 이것을 $\cos\frac{\beta}{2}$와 비교해도 동일한 결과를 얻을 수 있다.
- 하지만 위의 방법이 더 효율적이다.
(3) 조명 효과의 구현 #
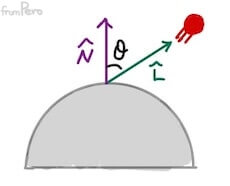
- 램버트 반사(Lambertian reflection)
- 표면에서의 조명 모델 계산을 위해 쓰인다.
- 빛을 받아서 표면에서 반사되는 빛의 세기는 두 벡터가 만드는 사잇각의 $cos$함수에 비례한다는 것이다. 즉, 사잇각이 커질 수록 $\cos$함수의 값이 적어져서 빛도 줄어든다는 것이다.
- 표면이 향하는 단위벡터 $\hat{N}$과 표면에서 광원으로 향하는 단위벡터 $\hat{L}$이 있다. 여기서 두 벡터를 내적하여 사잇각의 $\cos$값을 얻을 수 있다.
$$\hat{N} \cdot \hat{L} = \cos\theta$$
// circle에 존재하는 모든 픽셀 v에 대해 적용한다.
for (auto const& v : circle)
{
Vector2 n = (v - circlePosition).GetNormalize();
Vector2 l = (lightPosition - v).GetNormalize();
float shading = Math::Clamp(n.Dot(l), 0.f, 1.f); // 음수는 의미가 없으므로 0으로 만든다.
r.DrawPoint(v, lightColor * shading); // 빛의 색상과 shading을 곱해서 해당 픽셀에 적용한다.
}
(4) 투영 벡터 #
- 벡터의 내적은 어떤 벡터를 다른 벡터에 직교 투영하는 용도로도 사용된다.
- 예를 들면, 다음과 같이 카메라와 물체 사이의 깊이 값을 구할 때, 내적을 사용해서 투영 벡터를 구할 수 있겠다.
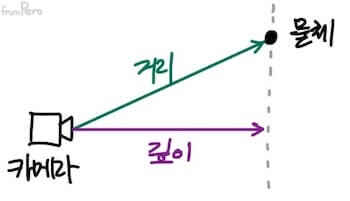
- 투영 벡터를 구하는 공식
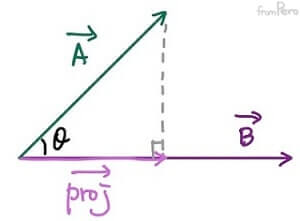
$$\vec{A} \cdot \vec{B} = |\vec{A}| \cdot |\vec{B}| \cdot \cos\theta = |\vec{A}| \cdot |\vec{B}| \cdot \frac{|\vec{proj}|}{|\vec{A}|} = |\vec{B}| \cdot |\vec{proj}|$$ $$|\vec{proj}| = \frac{\vec{A} \cdot \vec{B}}{|\vec{B}|}$$
- $\vec{proj}$는 $\vec{B}$와 방향이 같으므로 $|\vec{proj}| \cdot \hat{B}$으로도 표현할 수 있다.
$$\vec{proj} = |\vec{proj}| \cdot \hat{B}$$
- 여기에 맨 위의 공식을 대입하면 다음과 같다.
$$\vec{proj} = \frac{\vec{A} \cdot \vec{B}}{|\vec{B}|} \cdot \hat{B}$$ $$\vec{proj} = \frac{\vec{A} \cdot \vec{B}}{|\vec{B}|} \cdot \frac{\vec{B}}{|\vec{B}|} = \frac{\vec{A} \cdot \vec{B}}{|\vec{B}|^2} \cdot \vec{B}$$
- 여기서 $\vec{B}$ 크기를 $1$로 정규화 하면 다음과 같이 단순하게 정리할 수 있다.
$$\vec{proj} = (\vec{A} \cdot \hat{B}) \cdot \hat{B}$$
Vector2 unitB = (lineEnd - lineStart).GetNormalize();
Vector2 A = point - lineStart;
Vector2 proj = unitB * (A.Dot(unitB));
Vector2 projectedPoint = lineStart - proj;
float depth = (projectedPoint - point).Size();