[게임 수학] Chapter 6. 아핀 공간: 움직이는 가상 세계의 구축
Table of Contents
이득우의 게임 수학 책을 읽고 공부한 노트입니다.
이동 변환을 위한 아핀 공간 #
- 행렬 곱으로 어떻게 이동 기능을 구현할 수 있을까?
$$A \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x + a \\ y + b \end{bmatrix}$$
- 이러한 행렬 곱을 만족하는 정방행렬 $A$는 존재하지 않는다.
- 왜냐하면, 표준기저벡터의 원점을 이동시키기 위해서는 $A$가 선형성을 만족해야 한다. 그러나 선형성이 되기 위해서는 Chapter 5에서 본 것처럼 기저벡터가 원점에서 출발해야한다.
- 차원을 하나 더 늘려서 선형 변환을 위한 원점과의 연결고리로 활용하면 어떨까?
- 전단 변환을 생각해보자.
- 전단 변환으로 공간을 오른쪽으로 밀면, $y$값이 $1$인 영역의 $x$범위는 밀어낸만큼 이동한다.
- 따라서 다음과 같이 벡터의 $y$값을 $1$로 고정한다면 $x$를 이동시킬 수 있다.
$$\begin{bmatrix} 1 & a\\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ 1 \end{bmatrix} = \begin{bmatrix} x + a \\ 1 \end{bmatrix} $$
- 그렇다면, 2차원을 3차원으로 확장하고 마지막 차원 $z$값을 1로 고정한 전단 변환을 시행하면 $x$와 $y$를 이동시킬 수 있겠다.
$$\begin{bmatrix} 1 & 0 & a\\ 0 & 1 & b \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x + a \\ y + b \\ 1 \end{bmatrix} $$
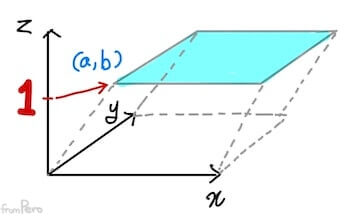
- 이동 변환행렬(Translate transformation matrix)
- 마지막 차원의 값이 1이라는 특정 조건을 가지는 전단 변환을 활용해서 이동 기능을 행렬로 구현한 것이다.
$$ T = \begin{bmatrix} 1 & 0 & a\\ 0 & 1 & b \\ 0 & 0 & 1 \end{bmatrix}$$
- 우리가 Chapter 5에서 보았던 크기와 회전 변환행렬의 경우 $2 \times 2$정방행렬이기 때문에 이동 변환행렬과 같이 $3 \times 3$으로 맞추어 줄 필요가 있겠다.
$$S = \begin{bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ $$R = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}$$
- 아핀 공간(Affine space)
- 벡터 공간에서 이동을 위해 마지막 차원 값을 $1$로 한정한 부분 공간을 말한다.
- 위의 그림에서 파란색으로 칠한 공간이다.
- 아핀 변환(Affine transformation)
- 한 차원을 높여서 설계해서 점, 직선, 평면을 보존하는 선형 변환을 말한다.
아핀 공간의 구성요소 #
- 점(Point)
- 물체를 표현하고 위치를 지정하는 요소
- 마지막 차원의 값은 항상 $1$이다.
- 예를 들어 $2$라면 이동 변환 시 $(x + 2a, y + 2b, 2)$와 같은 이상한 결과가 나올 것이다.
- 2차원 공간의 점 $$(x, y, 1)$$
- 3차원 공간의 점 $$(x, y, z, 1)$$
- 이동 벡터 혹은 변위 벡터 (Displacement vector)
- 물체를 움직이는 데 사용하는 요소.
- 마지막 차원의 값은 항상 $0$이다.
- 아핀 공간의 점 $P_1$에 이동 벡터 $\vec{v}$를 더한 결과는 아핀 공간의 다른 점 $P_2$에 대응된다.
$$P_1 + \vec{v} = P_2$$
$$\vec{v} = P_2 - P_1$$
- 여기서 벡터 $\vec{v}$는 $P_1$에서 $P_2$를 향하는 벡터를 의미한다. (순서를 거꾸로하면 반대로 향한다.)
- 점 $P_1$이 $(x_1, y_1, 1)$이고 $P_2$가 $(x_2, y_2, 1)$이라면 두 점을 빼서 만든 이동 벡터 $\vec{v}$의 마지막 차원 값은 $x$, $y$값과 무관하게 $0$이 됨을 알 수 있다. $$(x_1 - x_2, y_1 - y_2, 0)$$
아핀 공간의 성질 #
- 유클리드 공간(Euclidean space) → 아핀 공간에 대응된다
- 물리적인 관점에서 바라본 현실 세계의 3차원 공간이다.
- 유클리드 벡터(Euclidean vector) → 이동 벡터에 대응된다
- 유클리드 공간에서 작용하는 힘이다.
- 점과 이동 벡터의 마지막 차원 값을 토대로 다음과 같은 연산 규칙이 성립한다.
| 연산 규칙 | 마지막 차원 값 계산 |
|---|---|
| 점 $-$ 점 $=$ 벡터 | $(1 - 1 = 0)$ |
| 점 $+$ 벡터 $=$ 점 | $(1 + 0 = 1)$ |
| 벡터 $+$ 벡터 $=$ 벡터 | $(0 + 0 = 0)$ |
| 점 $+$ 점 $\neq$ 점 | $(1 + 1 = 2)$ 마지막 차원 값이 $2$가 되므로 아핀 공간 영역을 벗어나게 되어서 성립하지 않는다. |
아핀 결합 #
- 점 $+$ 점 $\neq$ 점 이다.
- 하지만 만약 선형 결합의 형태로 점에 스칼라를 곱한 후 더한다면 특정 조건에서 새로운 점을 생성하는 것이 가능하다.
- 점 $(x_1, y_1, 1)$과 $(x_2, y_2, 1)$에 각각 스칼라 $a$, $b$를 곱한 선형 결합은 다음과 같다.
$$a \cdot P_1 + b \cdot P_2 = (ax_1 + ax_2, ay_1 + by_2, a + b)$$
- 여기서 마지막 차원인 $a + b$가 $1$인 조건을 유지한다면 점과 점을 결합해서 새로운 점을 만들 수 있다.
- 동일한 원리로 점 세개를 가지고도 새로운 점을 만들 수 있다. $$a \cdot P_1 + b \cdot P_2 + c \cdot P_3 \ (s.t. \ a + b + c = 1)$$
- 아핀 결합(Affine combination)
- 이렇게 여러 개의 점을 결합해서 새로운 점을 생성하는 수식을 아핀 결합이라고 한다.
- $n$개의 점을 아핀 결합하는 경우
$$\displaystyle\sum_{i=1}^{n} c_i \cdot P_i (s.t. \displaystyle\sum_{i=1}^{n} c_i = 1)$$
두 점의 결합 #
- $b = 1 - a$을 대입하면, $a \cdot P_1 + (1 - a) \cdot P_2 = P’$이 된다.
- $a$에 $1$을 대입하면, 점 $P_1$이 생성된다.
- $a$에 $0$을 대입하면, 점 $P_2$가 생성된다.
- $a$에 $0.5$을 대입하면, 점 $P_1$과 $P_2$의 중점이 생성된다. $(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, 1)$
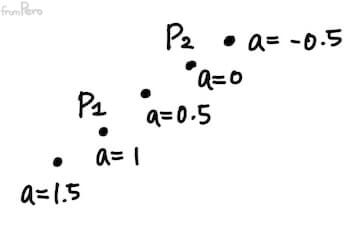
- 이렇듯 두 점 $P_1$, $P_2$의 아핀 결합으로 새로운 점을 생성하면 $a$값이 양의 방향으로 커질 수록 $P_1$의 바깥쪽에 점이 생성되고, $a$의 값이 음의 방향으로 커질 수록 $P_2$의 바깥쪽 방향에 점이 생성된다.
- 따라서 아핀 결합으로 생성되는 점을 모두 모으면 두 점 $P_1$, $P_2$을 지나는 무한한 긴 선이 만들어질 것이다.
- 이것을 수식으로 확인해보자.
- $a \cdot P_1 + (1 - a) \cdot P_2 = P’$을 $a$로 묶어서 다시 정리하면,
- $a(P_1 - P_2) = (P’ - P_2)$이다.
- 이것을 두 이동 벡터로 나타내면, $a \cdot \vec{u} = \vec{v}$이다.
- 이 식으로 두 벡터가 평행하다는 것을 알 수 있고, 따라서 아핀 결합으로 생성되는 점은 두 점을 지나는 직선 상에 위치함을 보장받게 된다.
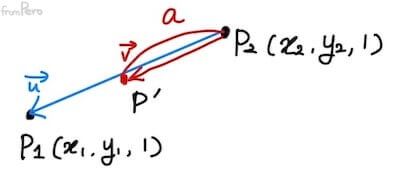
- 직선의 방정식
$$L(a) = a \cdot P_1 + (1 - a) \cdot P_2$$
- 직선의 방정식은 $a$의 범위에 따라 다양한 종류의 선에 대응된다.
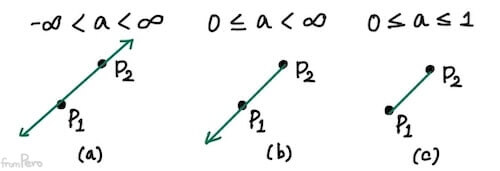
| 직선의 종류 | 설명 |
|---|---|
| (a) 직선(Line) | 양쪽 받향으로 무한히 뻗어나가는 선. 추상적인 선의 성질을 표현할 때 사용한다. |
| (b) 반직선(Ray) | 지정한 위치에서 한쪽으로만 뻗어나가는 선. 레이캐스팅(Raycasting), 레이트레이싱(Raytracing)에 사용된다. |
| (c) 선분(Line segment) | 시작점과 끝점의 위치가 정해져 있는 선. 프로그래밍을 활용해서 화면에 선을 그릴 때 사용한다. |
선 그리기 알고리즘 #
벡터를 모니터의 점으로 표현 #
- 데카르트 좌표계가 빈틈 없이 연속된(Continuous) 실수로 평면을 채우는 반면,
- 스크린 좌표계는 서로 독립된 영역을 가지는 이산적인(Discrete) 정수를 사용한다.
- 픽셀(Pixel)
- 스크린 좌표계를 사용해서 화면에 무언가를 표현하려면 스크린 좌표와 색상이 함께 지정되어야 한다. 이 때, 좌표와 색상에 대응하는 화면의 구성 요소를 픽셀이라고 한다.
- 픽셀화(Rasterization)
- 벡터를 화면의 점으로 표현하기 위해서 실수로 표현된 벡터 좌표를 정수로 변환한 후 색상을 부여하는 과정을 픽셀화라고 한다.
- 데카르트 좌표계와 스크린 좌표계의 차이
| 데카르트 좌표계 | 스크린 좌표계 | |
|---|---|---|
| 수 집합 | 실수 | 정수 |
| 수의 성질 | 연속성 | 이산성 |
| 단위 원소 | 벡터 | 픽셀 |
| 수의 범위 | 실수 범위 | $0$부터 해상도 크기까지 |
선 그리기 알고리즘 #
- 브레젠험 알고리즘(Bresenham’s algorithm)
- 화면을 8등분영역으로 구분한 후, 각 영역별로 그려내는 방식을 사용한다.
- 픽셀을 선택하기 위해서 중간값 $0.5$를 사용하기 때문에 중점 알고리즘(Midpoint algorithm) 이라고도 한다.
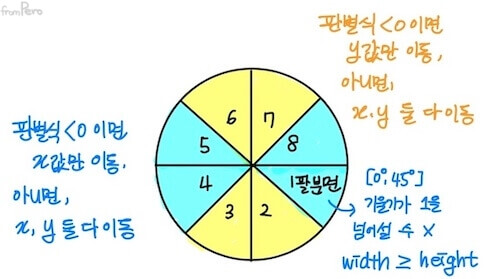
- 첫 번째 영역인 1팔분면(Octant)의 알고리즘을 만들어보자.
- 1팔분면은 $[0^\circ , 45^\circ]$의 범위를 가진다. 이것은 해당 영역에 존재하는 모든 선의 기울기 $\frac{h}{w}$ ($h$는 높이, $w$는 너비)가 $1$을 넘어설 수 없음을 의미한다.
- 시작 위치의 픽셀 $(x_0, y_0)$을 찍은 후에 그 다음 픽셀을 어디에 찍어야 할까?
- 1팔분면의 특성상 평행으로 이동하거나 아래로 한 칸 내려가게 될 것이다.
- 오른쪽으로 한 칸 이동한 $x$좌표는 $x_0 + 1$이 된다.
- $y$좌표는 평행($y_0$)이거나, 아래로 한 칸 내려갈($y_0 + 1$) 것이다. 둘 중에서 어떤 것일지 판단하기 위해서 중간값인 $y_0 + 0.5$를 사용한다. 즉, $y_0 + 0.5$를 기준으로 우리가 그리려는 $y$값이 더 작으면 수평으로 이동하고($y_0$), 그렇지 않으면 아래로 한 칸 내려가는($y_0 + 1$) 것이다.
- 이것을 직선의 방정식 $y = ax + b$을 사용해서 구하면 $2h - w < 0$이라는 판별식이 도출된다. (풀이 생략)
- $2h - w < 0$ 으로 다음 픽셀의 위치를 계산할 수 있게 됐다.
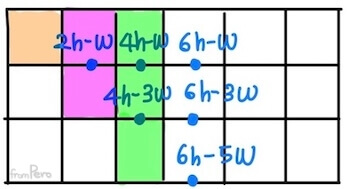
- 그 다음 픽셀은?
- 이전에 평행이동을 했다면, $(x_0 + 2, y_0 + 0.5)$을 직선의 방정식에 대입해서 판별식이 $4h - w < 0$이 된다.
- 이전에 아래로 내려갔다면, $(x_0 + 2, y_0 + 1.5)$을 직선의 방정식에 대입해서 판별식이 $4h - 3w < 0$이 된다.
- 이처럼 $x$값이 증가할 수록 판별식은 언제나 $2h$만큼 증가하며, 한 칸 내려갈 수록 $2w$만큼 줄어든다.
- 2팔분면은 1팔분면에서 $x$, $y$가 변경되었을 뿐 전개 방식은 동일하다.
- 3팔분면은 2팔분면에서 선분의 진행방향만 반대일 뿐 기본 원리는 동일하다.
- 따라서 다음과 같이 구현해 볼 수 있겠다.
void DrawLine(const Vector2& InStartPos, const Vector2& InEndPos, const LinearColor& InColor)
{
// 시작점과 끝점이 화면 영역을 벗어나면 클리핑 알고리즘을 수행한다(다음 절에서 살펴본다)
Vector2 clippedStart = InStartPos;
Vector2 clippedEnd = InEndPos;
Vector2 screenExtend = Vector2(_ScreenSize.X, _ScreenSize.Y) * 0.5f;
Vector2 minScreen = -screenExtend;
Vector2 maxScreen = screenExtend;
if (!CohenSutherlandLineClip(clippedStart, clippedEnd, minScreen, maxScreen))
{
return;
}
ScreenPoint startPosition = ScreenPoint::ToScreenCoordinate(_ScreenSize, clippedStart);
ScreenPoint endPosition = ScreenPoint::ToScreenCoordinate(_ScreenSize, clippedEnd);
int width = endPosition.X - startPosition.X;
int height = endPosition.Y - startPosition.Y;
// 완만한 경사(1, 4, 5, 8팔분면)인가? 아닌가(2, 3, 6, 7팔분면)?
bool isGradualSlope = (Math::Abs(width) >= Math::Abs(height));
// x, y축의 진행방향
int dx = (width >= 0) ? 1 : -1;
int dy = (height > 0) ? 1 : -1;
int fw = dx * width;
int fh = dy * height;
// 경사에 따른 판별식
int f = isGradualSlope ? fh * 2 - fw : 2 * fw - fh;
// 변화 없을 시 판별식에 적용할 값
int f1 = isGradualSlope ? 2 * fh : 2 * fw;
// 변화 있을 시 판별식에 적용할 값
int f2 = isGradualSlope ? 2 * (fh - fw) : 2 * (fw - fh);
// 최초 선 그리기 지점
int x = startPosition.X;
int y = startPosition.Y;
// 완만한 경사(1, 4, 5, 8)
if (isGradualSlope)
{
while (x != endPosition.X)
{
SetPixel(ScreenPoint(x, y), InColor);
if (f < 0) // 변화가 없는 경우
{
f += f1;
}
else. // 변화가 있는 경우
{
f += f2;
y += dy; // 변화가 있을 때만 y가 이동한다.
}
x += dx; // 언제나 x는 이동한다.
}
}
else // 급격한 경사(2, 3, 6, 7)
{
while (y != endPosition.Y)
{
SetPixel(ScreenPoint(x, y), InColor);
if (f < 0)
{
f += f1;
}
else
{
f += f2;
x += dx; // x, y가 완만한 경우와 반대이다.
}
y += dy;
}
}
}
라인 클리핑 알고리즘 #
- 클리핑(Clipping)
- 선분이 가진 성질은 유지하면서 지정된 영역에 맞는 데이터로 재설정하는 작업이다.
- 코헨-서덜랜드 라인 클리핑 알고리즘(Cohen-Sutherland line clipping algorithm)
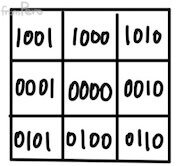
- 그릴 영역을 정 가운데에 두고 그 외의 바깥 영역을 포함해서 총 9개로 영역을 설정한다.
- 상위 두 비트는 상하 정보를, 하위 두 비트는 좌우 정보를 담아서 총 4자리의 이진수 값으로 고유한 값을 부여한다.
- 여기서 정 가운데의
0000이 눈에 보이는 화면 영역이다.
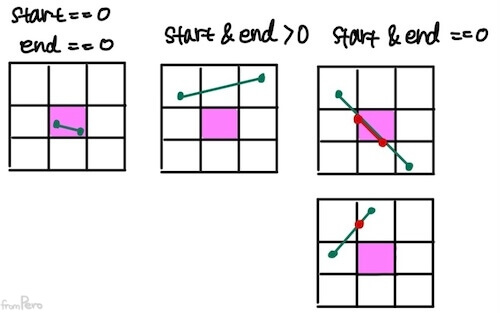
- 선분을 그릴 때 고려해야 할 상황은 세 가지로 나뉜다.
| 상황 | 특징 |
|---|---|
| (1) 화면 안에 위치해서 자를 필요가 없는 경우 |
시작점과 끝점 모두 0000이다. |
| (2) 화면 밖에 위치해서 그릴 필요가 없는 경우 |
시작점과 끝점의 &연산 결과가 $0$보다 큰 값이 나온다.혹은 $0$이 나올 때도 있다. 이 경우에는 클리핑을 한 후 다시 검사한다. |
| (3) 화면을 가로질러서 화면에 유효한 영역으로 잘라내야 하는 경우 |
시작점과 끝점의 &연산 결과가 $0$이 나온다. 따라서 클리핑을 한다. |
- 따라서 다음과 같이 구현해 볼 수 있겠다.
// 주어진 점의 영역값을 돌려준다.
int TestRegion(const Vector2& InVectorPos, const Vector2& InMinPos, const Vector2& InMaxPos)
{
int result = 0;
if (InVectorPos.X < InMinPos.X)
{
result = result | 0b0001;
}
else if (InVectorPos.X > InMaxPos.X)
{
result = result | 0b0010;
}
if (InVectorPos.Y < InMinPos.Y)
{
result = result | 0b0100;
}
else if (InVectorPos.Y > InMaxPos.Y)
{
result = result | 0b1000;
}
return result;
}
// 클리핑한다.
bool CohenSutherlandLineClip(Vector2& InOutStartPos, Vector2& InOutEndPos, const Vector2& InMinPos, const Vector2& InMaxPos)
{
int startTest = TestRegion(InOutStartPos, InMinPos, InMaxPos);
int endTest = TestRegion(InOutEndPos, InMinPos, InMaxPos);
float width = (InOutEndPos.X - InOutStartPos.X);
float height = (InOutEndPos.Y - InOutStartPos.Y);
while (true)
{
if ((startTest == 0) && (endTest == 0)) // 화면 안에 두 점이 있으면 바로 그리기
{
return true;
}
else if (startTest & endTest) // 화면 밖에 선이 있으므로 그릴 필요가 없음
{
return false;
}
else // 양쪽을 조사해 클리핑 진행
{
Vector2 clippedPosition;
bool isStartTest = (startTest != 0);
int currentTest = isStartTest ? startTest : endTest;
if (currentTest < 0b0100)
{
if (currentTest & 1)
{
clippedPosition.X = InMinPos.X;
}
else
{
clippedPosition.X = InMaxPos.X;
}
if (Math::EqualsInTolerance(height, 0.0f))
{
clippedPosition.Y = InOutStartPos.Y;
}
else
{
clippedPosition.Y = InOutStartPos.Y + height * (clippedPosition.X - InOutStartPos.X) / width;
}
}
else
{
if (currentTest & 0b0100)
{
clippedPosition.Y = InMinPos.Y;
}
else
{
clippedPosition.Y = InMaxPos.Y;
}
if (Math::EqualsInTolerance(width, 0.0f))
{
clippedPosition.X = InOutStartPos.X;
}
else
{
clippedPosition.X = InOutStartPos.X + width * (clippedPosition.Y - InOutStartPos.Y) / height;
}
}
// 클리핑한 결과로 다시 테스트 진행.
if (isStartTest)
{
InOutStartPos = clippedPosition;
startTest = TestRegion(InOutStartPos, InMinPos, InMaxPos);
}
else
{
InOutEndPos = clippedPosition;
endTest = TestRegion(InOutEndPos, InMinPos, InMaxPos);
}
}
}
return true;
}