↓Skip to main content

[Game Math] Chapter 5. 행렬: 가상 세계의 변환 도구

Table of Contents

이득우의 게임 수학 책을 읽고 공부한 노트입니다.



선형성: 예측 가능한 비례 관계 #

  • 선형성(Linearity) 이란?
    • 직선의 형태를 띠는 성질을 의미한다.
  • 함수 $f$에 대해 다음 두 가지 조건을 만족하면 함수 $f$는 선형이라고 한다.
  • (1) 가법성(Additivity)
    • 임의의 수 $x_1$, $x_2$에 대해

$$f(x_1 + x_2) = f(x_1) + f(x_2)$$

  • (2) 1차 동차성(Homogeneity)
    • 임의의 수 $x$, $k$에 대해

$$f(kx) = kf(x)$$


선형 함수 #

  • 직선의 함수 $f(x) = ax$의 경우
    • 가법성
      • $a(x_1 + x_2) = ax_1 + ax_2$이므로, $a$, $x_1$, $x_2$가 모두 체의 성질을 가지는 실수라면 분배법칙이 성립해서 OK
    • 1차 동시성
      • $a(kx) = k(ax)$이므로, $a$, $x$, $k$가 모두 체의 성질을 가지는 실수라면 체는 곱셈에 대해 결합법칙과 교환법칙이 성립하므로 OK

  • 곡선의 형태를 띠는 $f(x) = x^2$의 경우
    • 가법성
      • $x_1^2 + x_2^2 + 2x_1x_2 = x_1^2 x_2^2$이므로 NO

  • 스칼라 $b$를 더해본 $f(x) = ax + b$의 경우
    • 가법성
      • $ax_1 + ax_2 + b = ax_1 + b + ax_2 + b$이므로 NO
      • 어째서 직선의 형태를 띰에도 선형성을 만족하지 않을까?

  • 선형성이란 두 집합의 순수한 비로 구성된 1차적 대응 관계를 의미한다.
    • 단지 곧게 뻗은 직선의 성질을 뜻하는 것이 아니다.
    • 순수한 비로 구성되어 있기 때문에 다른 입력값을 투여했을 때 어떤 출력값이 나올지 쉽게 예측할 수 있고,
    • 반대로 역함수($f(x) = \frac{1}{a}x$)를 사용해서 출력값으로부터 입력값을 계산하는 것이 가능하다.
    • 따라서 원점에서 벗어난 $f(x) = ax + b$의 경우 선형성을 만족하지 못한다.

벡터 공간의 선형 변환 #

  • 그렇다면, 입력과 출력을 실수가 아닌 벡터를 넣어보자!
    • 선형성을 가지는 함수는 순수한 비의 형태로 구성되어 있으므로, $\vec{v} = (x, y)$에서 $x$와 $y$에 선형성을 유지하고자 한다면 다음과 같이 설계해 볼 수 있겠다.
  • $f(\vec{v}) = f(x, y) = (ax + by, cx + dy)$
    • 이 식은 가법성과 1차 동차성을 만족하므로 선형성을 지닌다. (풀이 생략)
      • 따라서 순수한 비를 통해 예측할 수 있는 형태로 변환되며,
      • 역함수를 통해 변환 후의 벡터로부터 변환 전의 벡터를 파악할 수 있다.
  • 표준기저벡터의 선형 결합으로 형성된 벡터 공간은 선형성을 지닌다. 그리고 이 벡터 공간을 위와 같은 선형 함수를 이용해서 변화시킨 새로운 공간도 표준기저벡터의 선형 결합으로 형성되므로 선형성을 지니겠다.
    • 이렇게 동일한 구조를 지니는 두 공간의 대응관계를 변환(Transformation)이라고 하며,
    • 선형성을 유지시켜주는 위와같은 선형 함수를 선형 변환(Linear transformation) 이라고 한다.

  • 스칼라 곱셈 $f(\vec{v}) = f(x, y) = (kx, ky)$의 경우
    • $(ax + by, cx + dy)$에다가 $a = k, b = 0, c = 0, d = k$를 대입한 것이므로, 선형변환이다.
  • 벡터를 회전시키는 $f(\vec{v}) = f(x, y) = (\cos\theta x - \sin\theta y, \cos\theta x + \sin\theta y)$의 경우
    • $(ax + by, cx + dy)$에다가 $a = \cos\theta, b = - \sin\theta, c = \cos\theta, d = \sin\theta$를 대입한 것이므로, 선형변환이다.

  • 게임 세계에서 모든 변환들은 선형 변환에 기초를 두고 있다.
    • 이런 선형 변환의 계산 과정을 체계화해서 손쉽게 계산할 수 있다면 좋겠다!
      • 그것이 바로 행렬(Matrix) 이다.



행렬 #

  • 행렬은 수를 사각형의 형태로 행과 열을 맞춰 배열한 테이블이다.
  • 행렬을 사용해서 벡터를 나타낼 수 있다.
명칭 표기 방식
열벡터 $$ \begin{bmatrix} x \\ y \end{bmatrix} $$
행벡터 $$ \begin{bmatrix} x & y \end{bmatrix} $$
  • 선형변환을 표현할 때는 행과 열의 크기가 같은 정방행렬(Square matrix) 을 사용한다.
  • $f(x, y) = (ax + by, cx + dy)$의 경우에는 $$\begin{bmatrix} a & b \\ c & d \end{bmatrix}$$ 와 같이 표현할 수 있겠다.

행렬의 기본 연산 #

  • 반드시 알아야 하는 행렬의 연산들
  • (1) 행렬과 행렬의 덧셈

$$A + B = \begin{bmatrix} a & b \\ c & d \end{bmatrix} + \begin{bmatrix} e & f \\ g & h \end{bmatrix} = \begin{bmatrix} a+e & b+f \\ c+g & d+h \end{bmatrix} $$

  • (2) 행렬과 스칼라의 곱셈

$$k \cdot A = k \cdot \begin{bmatrix} a & b \\ c & d \end{bmatrix} = \begin{bmatrix} k \cdot a & k \cdot b \\ k \cdot c & k \cdot d \end{bmatrix} $$

  • (3) 행렬의 전치(Transpose of a matrix)
    • 첨자 $T$으로 표시하며, 행과 열을 바꾸는 연산이다.

$$\begin{bmatrix} a & d \\ b & e \\ c & f \end{bmatrix}^T = \begin{bmatrix} a & b & c \\ d & e & f \end{bmatrix}$$

  • (4) 행렬과 행렬의 곱셈 (행렬 곱)
    • (이어서..)

행렬과 행렬의 곱셈 #

  • 앞의 행벡터와 뒤의 열벡터를 각각 곱해서 더한다.

$$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot \begin{bmatrix} e & f \\ g & h \end{bmatrix} = \begin{bmatrix} ae + bg & af + bh \\ ce + dg & cf + dh \end{bmatrix}$$


  • 교환법칙이 성립하지 않는다.

$$A \cdot B \neq B \cdot A$$

  • 결합법칙이 성립한다.

$$A \cdot (B \cdot C) = (A \cdot B) \cdot C$$

  • 행렬 곱을 전치한 결과는 순서를 바꾼 후 각각 전치해서 곱한 결과와 동일하다.

$$(A \cdot B)^T = B^T \cdot A^T$$


  • 앞서서 본 선형 함수 $f(x, y) = (ax + by, cx + dy)$ 를 행렬로 표현하면 다음과 같다. $$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix}$$
    • 2차원 벡터에 선형 변환을 적용해서 새로운 벡터를 생성하는 작업이라고 볼 수 있다.
    • 연산의 순서는 오른쪽에서 왼쪽으로 역방향으로 이루어짐을 알 수 있다.

정방행렬의 곱셈 #

  • $2 \times 2$정방행렬 간의 곱은 합성함수에 대응되는 연산이다.
  • 벡터 $\vec{v}$에 선형 변환을 나타내는 $2 \times 2$정방행렬 $A$, $B$를 순서대로 연산하는 것은 다음과 같다.

$$B \cdot A \cdot \vec{v}$$


  • 행렬의 곱셈은 결합법칙이 성립하기 때문에 컴퓨터 그래픽 연산에서 계산량을 크게 줄일 수 있다.
    • 예를 들어, 100개의 점을 5번씩 선형 변환($A$, $B$, $C$, $D$, $E$)을 한다고 하면,
    • $E \cdot D \cdot C \cdot B \cdot A \cdot \vec{v_1}$과 같은 작업이 100번 이루어지며, 총 500번의 행렬곱 연산이 필요하다.
    • 하지만 $F = E \cdot D \cdot C \cdot B \cdot A$와 같이 합성함수에 해당하는 $F$를 미리 만들어 두면, $F \cdot \vec{v_1}$과 같이 점 당 한 번씩만 행렬곱을 하면 된다. 그래서 총 104번의 행렬곱 연산만 하면 된다.

열 기준 행렬과 행 기준 행렬 #

  • 행렬과 벡터의 곱셈을 서로 다른 방식으로 수행한다.
명칭 설명
열 기준 행렬 역방향으로 연산된다.
사례: DirectX, Unity
$$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix}$$
행 기준 행렬 순방향으로 연산된다.
사례: OpenGL, Unreal
열 기준 행렬에 전치연산을 적용하면 된다.
$(A \cdot \vec{v})^T = \vec{v}^T \cdot A^T$
$$\begin{bmatrix} x & y \end{bmatrix} \cdot \begin{bmatrix} a & c \\ b & d \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix}$$



행렬의 설계 #

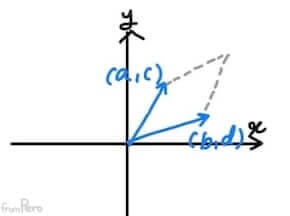
  • 평면 상의 물체를 원하는 대로 변환하기 위해 $2 \times 2$행렬을 설계해보자.

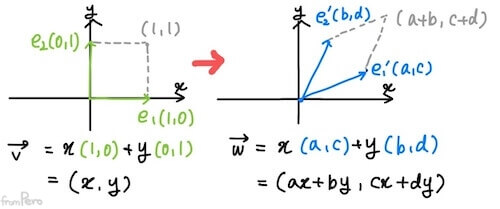
선형 변환을 통한 기저벡터의 변화 alt ><

  • 위 그림과 같이 표준기저벡터를 변화시켜서 벡터와 선형 결합을 하면 $$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix}$$와 동일한 값을 가진다.
    • 따라서 표준기저벡터를 변화시킨 벡터인 $(a, c)$와 $(b, d)$는 정방행렬을 구성하는 열벡터임을 알 수 있다.

크기 변환행렬 #

  • 크기 변환행렬(Scale transformation matrix)
  • 물체를 크기를 변경하는 행렬을 설계해보자.

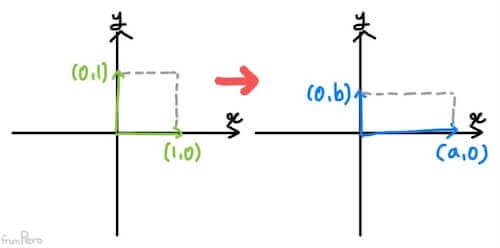
크기 변환행렬 alt ><

  • 표준기저벡터 $e_1$을 $a$배 늘리거나 줄인 벡터

$$a \cdot (1, 0) = (a, 0)$$

  • 표준기저벡터 $e_2$을 $b$배 늘리거나 줄인 벡터

$$b \cdot (0, 1) = (0, b)$$

  • 이 두 표준기저벡터를 열벡터로 설정하면 다음과 같은 크기 변환행렬을 만들 수 있겠다.

$$S = \begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix}$$


회전 변환행렬 #

  • 회전 변환행렬(Rotation transformation matrix)
  • 물체를 각 $\theta$만큼 회전시키는 행렬을 설계해보자.

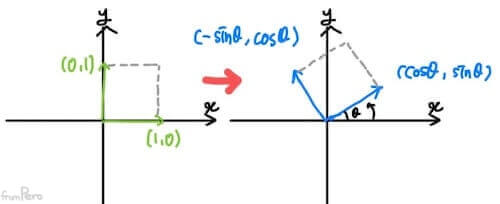
회전 변환행렬 alt ><

  • Chapter 4에서 살펴본 바와 같이 표준기저벡터가 $\theta$만큼 회전한 결과는 $(\cos\theta, \sin\theta)$와 $(-\sin\theta, \cos\theta)$가 된다.
  • 따라서 이 두 표준기저벡터를 열벡터로 설정해서 다음과 같은 회전 변환행렬을 만들 수 있겠다.

$$R_\theta = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}$$


전단 변환행렬 #

  • 전단 변환행렬(Shear transformation matrix)
  • 표준기저벡터 $e_1$은 고정한 상태에서 $e_2$를 $x$축 방향으로 $a$만큼 미는 변환을 생각해보자.

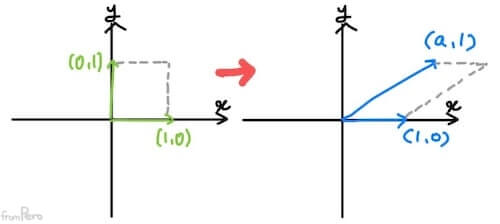
전단 변환행렬 alt ><

  • 이러한 것을 전단변환이라고 하며, 전단변환행렬은 다음과 같을 것이다.

$$S = \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix}$$


삼각함수의 덧셈 정리 #

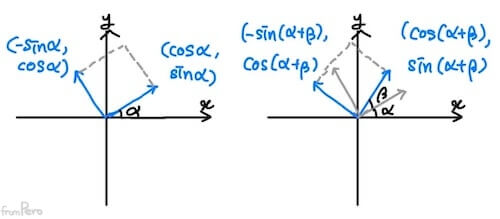
두 회전을 합성한 변환 alt ><

  • 위 그림과 같이 $\alpha$와 $\beta$를 합한 만큼 회전한 행렬은 다음과 같이 나타낼 수 있다.

$$R_(\alpha + \beta) = \begin{bmatrix} \cos(\alpha + \beta) & -\sin(\alpha + \beta) \\ \sin(\alpha + \beta) & \cos(\alpha + \beta) \end{bmatrix}$$


  • 여기서 $\alpha + \beta$의 회전변환은 $\alpha$만큼 회전한 후, $\beta$만큼 회전한 것과 같다. 따라서 다음과 같은 결과가 나온다.

$$R_\beta \cdot R_\alpha = \begin{bmatrix} \cos(\beta) & -\sin(\beta) \\ \sin(\beta) & \cos(\beta) \end{bmatrix} \begin{bmatrix} \cos(\alpha) & -\sin(\alpha) \\ \sin(\alpha) & \cos(\alpha) \end{bmatrix}$$ $$ = \begin{bmatrix} \cos\alpha\cos\beta - \sin\alpha\sin\beta & -(\cos\alpha\sin\beta + \sin\alpha\cos\beta) \\ \cos\alpha\sin\beta + \sin\alpha\cos\beta & \cos\alpha\cos\beta-\sin\alpha\sin\beta \end{bmatrix}$$


  • 여기서 삼각함수의 덧셈 정리를 얻을 수 있다.

$$\cos(\alpha + \beta) = \cos\alpha\cos\beta- \sin\alpha\sin\beta$$ $$\sin(\alpha + \beta) = \cos\alpha\sin\beta + \sin\alpha\cos\beta$$


  • 추가적으로 삼각함수의 배각 공식은 각 $\beta$대신 $\alpha$를 대입해서 얻을 수 있다.

$$\cos 2 \alpha = 1 - 2 \sin^2 \alpha$$ $$\sin 2 \alpha = 2 \sin \alpha \cos \alpha$$



역행렬 #

  • 행렬은 본질적으로 함수의 성질을 지니기 때문에 항등행렬과 역행렬이라는 개념이 존재한다.

  • 항등행렬(Identity matrix)
    • 원 공간의 변화없이 동일한 공간으로 유지하는 변환을 의미한다.
    • 표준기저벡터 $(1, 0)$과 $(0, 1)$을 순서대로 넣어 만들 수 있다.

$$I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$


  • 역행렬(Inverse matrix)
    • 행렬 곱의 결과가 항등행렬이 나오는 행렬을 의미한다.

$$A \cdot A^{-1} = A^{-1} \cdot A = I$$

  • 역행렬을 시각적으로 나타내본다면, 아래 그림과 같이 선형 변환된 벡터 공간을 원 벡터 공간으로 되돌리는 선형 변환이라고 볼 수 있다.

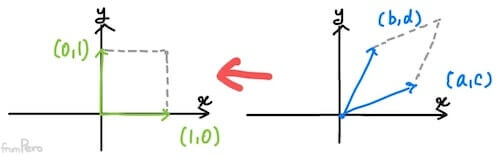
두 회전을 합성한 변환 alt ><


역행렬의 존재를 판별하는 성립식 #

  • 역행렬 또한 함수이므로, 두 공간의 변환이 전단사로 대응될 때만 역행렬이 존재한다.
    • 역행렬이 존재하는지 파악할 수 있는 특별한 수식이 있는 데 이것을 행렬식(Determinant) 이라고 한다.
  • $2 \times 2$정방행렬 $A$의 행렬식은 다음과 같이 계산한다. $$A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$$
    • $det(A) = ad - bc$
    • $det(A)$의 값이 $0$인 선형 변환은 전단사 대응이 성립하지 않아서 역행렬이 존재하지 않는다.

  • 행렬식이 $0$이라는 것의 의미는 무엇일까?
  • 임의의 행렬 $$A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$$를 사용해서 표준기저벡터가 $(a, c)$와 $(b, d)$로 변환된, 새로운 벡터 공간의 넒이는 어떻게 될까?

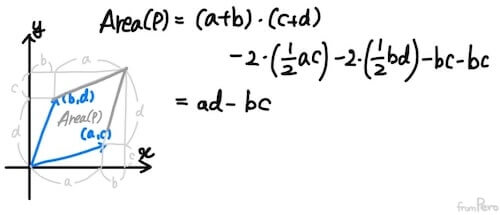
평행사변형의 넓이 alt ><

  • 넓이 $Area(P)$는 전체 사각형의 넓이에서 평행사변형을 제외한 삼각형과 사각형을 빼서 구할 수 있으며, 결과적으로 행렬식과 동일하게 된다.
  • $Area(P) = ad - bc$
  • 따라서 이 넓이가 $0$이라는 것은 2차원의 평면 영역이 1차원의 직선 영역으로 압축되었다는 것을 뜻하며, 그렇기 때문에 다시 2차원으로 돌아갈 수 없게되는 것이다.

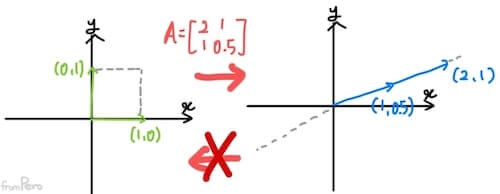
행렬식이 0인 경우 alt ><


  • 행렬식이 음수가 나온다면?
    • $ad - bc$에서 모든 수가 양수일 때 $a < b$이고, $d < c$이면 계산 결과는 음수가 나온다.
    • 이것은 두 표준기저벡터가 엇갈리면서 평면이 뒤집힌 것이라고 볼 수 있다.

행렬식이 음수인 경우 alt &gt;&lt;


크기 변환행렬의 역행렬 #

$$S = \begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix}$$

$$S^{-1} = \begin{bmatrix} \frac{1}{a} & 0 \\ 0 & \frac{1}{b} \end{bmatrix}$$


회전 변환행렬의 역행렬 #

  • Chapter 4에서 보았던 $\cos$, $\sin$ 함수의 짝함수, 홀함수 성질을 사용해서 역행렬을 구할 수가 있겠다.
    • 짝함수 : $\cos(-\theta) = \cos(\theta)$
    • 홀함수 : $\sin(\theta) = -\sin(\theta)$

$$R_{\theta} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}$$

$$R_{\theta}^{-1} = R_{(-\theta)} = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix}$$


  • 가만보니 이 결과는 전치행렬과 동일하다.
    • 따라서 회전 변환행렬의 역행렬은 전치연산을 적용하는 방법으로 쉽게 구할 수 있겠다.

$$R_{\theta}^{-1} = R_{\theta}^{T}$$


전단 변환행렬의 역행렬 #

$$S = \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix}$$

$$S^{-1} = \begin{bmatrix} 1 & -a \\ 0 & 1 \end{bmatrix}$$


행렬 곱의 역행렬 #

  • 행렬 곱은 합성 함수이므로 다음과 같은 수식이 성립한다.

$$(g \circ f)^{-1} = f^{-1} \circ g^{-1}$$ $$(A \cdot B)^{-1} = B^{-1} \cdot A^{-1}$$



↑