↓Skip to main content

[Game Math] Chapter 4. 삼각함수: 회전을 위한 수학

Table of Contents

이득우의 게임 수학 책을 읽고 공부한 노트입니다.



삼각함수 #

  • 삼각비(Trigonometric ratio)
    • 직각삼각형을 구성하는 세 변에서, 직각이 아닌 각에 대한 두 변의 비례관계를 나타낸 것이다.

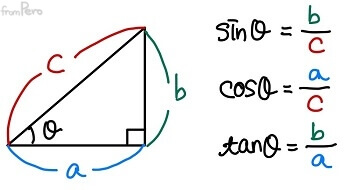
삼각비 alt ><

  • 삼각비를 구하려면 꼭 직각삼각형이어야 하므로, $\theta$는 늘 $0^\circ$와 $90^\circ$ 사이이다.
    • 그렇다면 $90^\circ$를 넘어서는 각에 대해서는 어떻게 삼각비를 구할 수 있을까?

  • 삼각함수(Trigonometric function)
    • 각의 크기를 삼각비로 나타내는 함수이다.
    • 직각삼각형을 데카르트 좌표계 상에 배치하고, 사잇각의 범위를 실수 전체인 $\mathbb{R^2}$집합으로 확장하였다.
  • 반지름이 $1$인 원을 사용하면 삼각함수를 좀 더 쉽게 파악할 수 있다.
    • $\sin\theta = \frac{b}{1} = b$이고, $\cos\theta = \frac{a}{1} = a$이므로, 원주 위의 모든 좌표는 $(\cos\theta, \sin\theta)$에 대응한다.

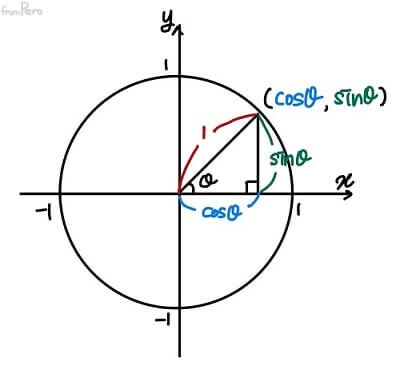
삼각함수 alt ><

  • 이것을 피타고라스 정리에 대입하면, $\cos^2\theta + \sin^2\theta = 1$과 같은 공식을 얻을 수 있다.
    • 이번에는 반지름을 $r$으로 일반화시켜 생각해보자.
    • 벡터의 개념으로 생각했을 때, 길이가 $1$에서 $r$만큼 증가 했으므로, 스칼라 곱셈에 의해 $r\cdot(\cos\theta, \sin\theta)$라는 좌표를 얻을 수 있다.
    • 따라서 밑변과 높이는 각각 $r\cdot\cos\theta$와 $r\cdot\sin\theta$가 된다.
    • 이것을 피타고라스 정리에 대입하면, $r^2(\cos^2\theta + \sin^2\theta) = r^2$이므로, 반지름 길이와 무관하게 $\cos^2\theta + \sin^2\theta = 1$식은 성립한다.

삼각함수의 성질 #

  • 데카르트 좌표계에서의 각도란?
    • $x$축에서 원의 궤적을 따라 반시계 방향으로 회전한 크기를 의미한다.

  • 반지름이 $1$인 단위 원에서 반시계 방향의 회전을 생각해보자.
    • 아직 회전하지 않은 상태에서 빗변 $\vec{v}$는 $x$축에 위치하며, 좌표는 $(1, 0)$이다. 이것의 각도는 $0^\circ$이겠다.
    • 여기서 각도를 서서히 증가시키다면?
    • 각도에 따른 $v_x$와 $v_y$의 변화량을 나타낸 $\cos\theta$와 $\sin\theta$ 함수는 아래 그래프와 같이 나올 것이다.
    • 값의 변화는 $[-1, 1]$범위(진폭: Amplitude) 내에서 $360^\circ$마다 반복(주기: Period)된다.

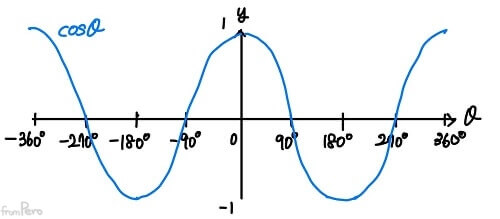
cos함수그래프 alt ><

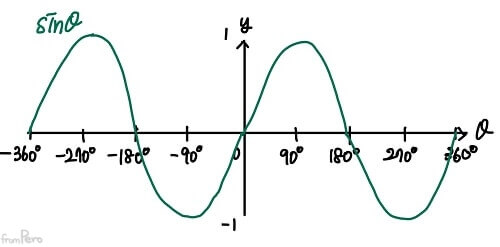
sin함수그래프 alt ><


  • 짝함수와 홀함수
명칭 설명
짝함수
(Even function)		 $y$축을 기준으로 좌우를 접었을 때 $\cos$함수와 같이 좌우 대칭인 함수.
$\cos(-\theta) = \cos(\theta)$
홀함수
(Odd function)		 $y$축을 기준으로 좌우를 접었을 때 $\sin$함수와 같이 원점 대칭인 함수.
$\sin(-\theta) = -\sin(\theta)$

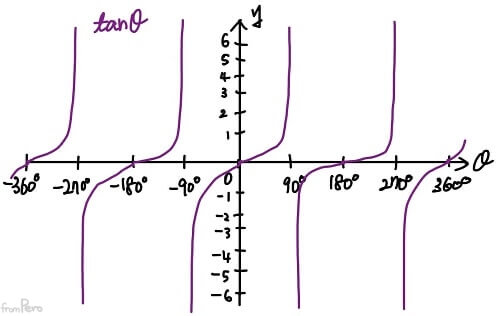
  • $\tan$함수의 특징
    • 빗변과 무관하게 밑변과 높이의 관계만을 나타낸다. $$\tan\theta = \frac{b}{a}$$
    • 분자와 분모를 모두 빗변 값으로 나누면? $$\tan\theta = \frac{\frac{b}{c}}{\frac{a}{c}} = \frac{\sin\theta}{\cos\theta}$$
    • 분모의 값은 $0$이 될 수 없기 때문에, 분모인 $\cos$함수의 값이 $0$이 되는 각도(예를 들면, $90^\circ$)에서는 $\tan$값이 존재하지 않는다.
    • $\sin$함수처럼 홀함수의 성질을 지닌다.

tan함수그래프 alt ><


각의 측정법 #

  • 각도법(Degree)
    • 우리가 일상생활에서 사용하듯이 $0$에서 $360$까지의 수를 사용하는 방법이다.
  • 호도법(Radian)
    • 호의 길이를 기준으로 각을 측정하는 방법이다.
    • 크기 1인 단위벡터를 사용해서 크기를 비교하는 것처럼, 호의 길이가 1이 되는 부채꼴의 각을 기준으로 각을 측정한다.

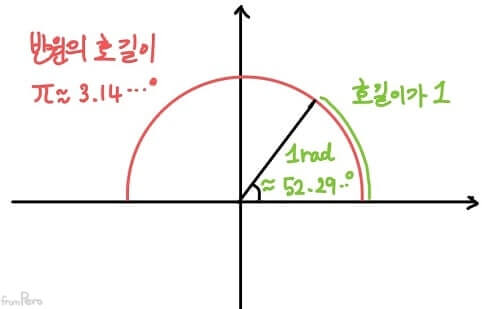
호도법 alt ><

  • 반원($180^\circ$)의 호길이는 $\pi$이므로 다음과 같은 변환식을 만들 수 있다.
    $1^\circ = \frac{\pi}{180} (rad)$
    $1 (rad) = (\frac{180}{\pi})^\circ$



삼각함수를 활용한 물체의 회전 #

  • 물체를 이동시키고, 크기를 늘리는 것은 $x$축과 $y$축이 서로 독립적으로 적용된다. 따라서 이 두 축을 서로 분리해서 따로 계산한 후 결합한 것과 동일하다.
  • 하지만 회전은 $x$와 $y$값이 함께 영향을 미치기 때문에 분리해서 독립적으로 계산할 수 없다.

  • 기저벡터 개념을 활용해서 회전시켜보자.
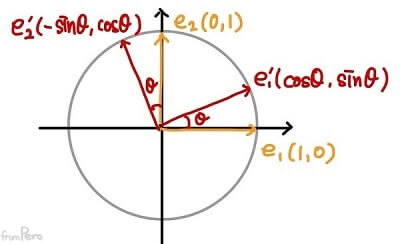
  • $\mathbb{R^2}$의 기저벡터 $e_1 = (1, 0)$과 $e_2 = (0, 1)$을 각 $\theta$만큼 회전시키면?
    • $e_1’ = (\cos\theta, \sin\theta)$과 $e_2’ = (-\sin\theta, \cos\theta)$가 될 것이다.

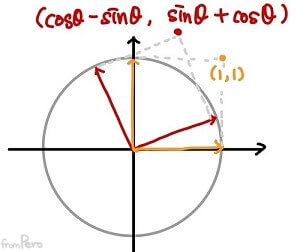
기저벡터의 회전 alt ><

  • $(1, 1)$에 위치한 벡터 $\vec{v}$는 $\vec{v} = 1 \cdot e_1 + 1 \cdot e_2$라고 표현할 수 있다.

  • 이 벡터를 $\theta$만큼 회전시키면?
    • $\vec{v}’ = 1 \cdot (\cos\theta, \sin\theta) + 1 \cdot (-\sin\theta, \cos\theta)$이며
    • 따라서 $\vec{v}’ = (\cos\theta - \sin\theta, \sin\theta + \cos\theta)$가 된다.

벡터의 회전 alt ><


  • 이것을 일반화시킨다면, $(x, y)$에 위치한 벡터를 $\theta$만큼 회전한 $(x’, y’)$는 다음과 같다.
    $x’ = x\cos\theta - y\sin\theta$
    $y’ = x\sin\theta + y\cos\theta$



삼각함수의 역함수 #

  • 벡터의 좌표를 가지고 대응하는 각도를 알아내는 법은?
    • 각 삼각함수의 정의역과 공역의 범위를 제한시키면 전단사함수를 만들 수 있다. 이것은 역함수도 구할 수 있다는 것을 의미한다.
    • $\sin$함수가 $\theta$값이 주어졌을 때 두 변의 비례관계를 구하는 것이라면,
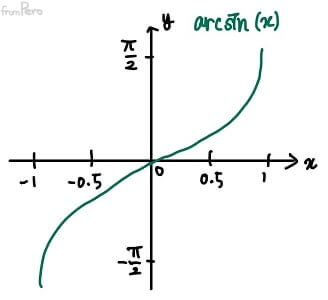
    • $\arcsin$함수는 거꾸로 $\sin$함수의 값인 두 변의 비례관계가 주어지면, 그것을 통해 $\theta$ 값을 구할 수 있는 것이다.

  • $\sin^{-1}(x) = \arcsin(x)$
    • 정의역: $[-90^\circ, 90^\circ]$
    • 공역: $[-1, 1]$

arcsin alt ><


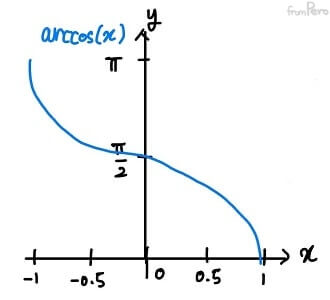
  • $\cos^{-1}(x) = \arccos(x)$
    • 정의역: $[0^\circ, 180^\circ]$
    • 공역: $[-1, 1]$

arccos alt ><


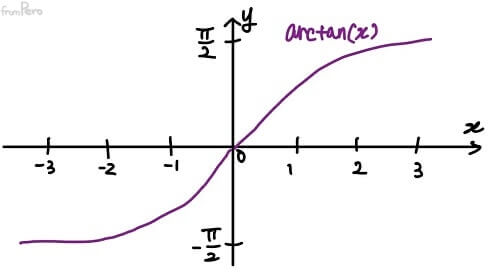
  • $\tan^{-1}(x) = \arctan(x)$
    • 정의역: $(-90^\circ, 90^\circ)$
    • 공역: 실수 영역 전체

arctan alt ><


  • $\arctan$ 함수는 벡터의 각도를 구하는 데 유용하게 사용할 수 있다.

    • $\vec{v} = (x, y)$라는 임의의 벡터가 있을 때, $\tan\theta$는 $\frac{y}{x}$이다. 이 값을 이용해서 $\arctan$함수로 $\theta$에 해당하는 각도값을 구할 수 있다.
    • 하지만! $\arctan$함수는 정의역이 $(-90^\circ, 90^\circ)$으로 한정되어 있다는 문제가 있다.
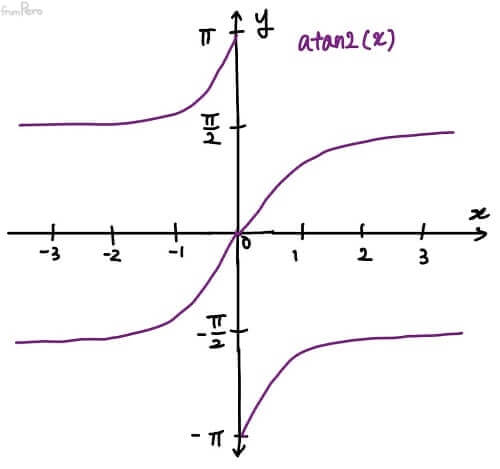
    • 따라서 각 축인 $x$와 $y$를 따로 분리해서 전달하는 함수인 $atan2$함수를 사용한다.

  • $atan2(y, x)$

    • 정의역: $[-180^\circ, 180^\circ]$
    • 공역: 실수 영역 전체

atan2 alt ><



극좌표계 #

  • 데카르트 좌표계
    • 앞에서 본 것처럼 회전을 구현하면 회전에 따른 $x$, $y$의 변화를 매번 계산하는 번거로움이 발생한다.
  • 극좌표계(Polar coordinate system)
    • 원점으로부터의 거리 $r$과, 각 $\theta$의 두 요소로 구성된다.
    • 극좌표계는 원형공간의 특징을 지닌다. 따라서 스킬 쿨타임 아이콘 등 회전에 관련된 효과를 줄 때 많이 사용된다.

$$(r, \theta)$$

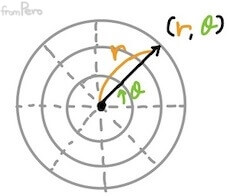
극좌표계 alt ><


  • 데카르트 좌표계 → 극좌표계로 변환
    $r = \sqrt{x^2 + y^2}$
    $\theta = atan2(x, y)$

  • 극좌표계 → 데카르트 좌표계로 변환
    $x = r \cdot \cos\theta$
    $y = r \cdot \sin\theta$



↑