[Algorithm] 수학적 개념과 알고리즘

Table of Contents

비트 조작 #

비트 조작 트릭 #

0s는 모든 비트가 0인 값이며, 1s는 모든 비트가 1인 값이다.

x ^ 0s = x    x & 0s = 0    x | 0s = x
x ^ 1s = ~x   x & 1s = x    x | 1s = 1s
x ^ x  = 0    x & x  = x    x | x  = x

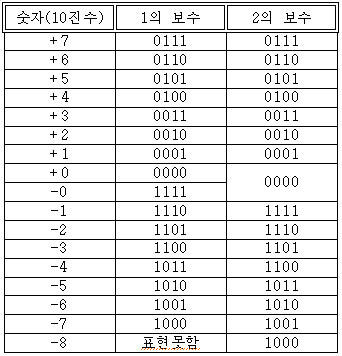
음수를 나타내기 위한 2의 보수법 #

보수(Complementary Number) 란?
- 보충을 해주는 수이다.
$R$진수에서, $N$에 대한 $R-1$의 보수란?
- $N$이 $R$진수에서 해당 자릿수의 최대값이 되기 위해 얼마를 보충해 주어야 하는 가이다.
$R$진수에서, $N$에 대한 $R$의 보수란?
- $N$이 $R$진수에서 자릿수를 한 자리 높이기 위헤 얼마를 보충해 주어야 하는 가이다.
- 이것은 $R-1$의 보수 $+ 1$ 과 같다.
예시
- $10$진수에서, $33$에 대한 $9$의 보수는?
  - $99 - 33 = 66$이다.
- $10$진수에서, $33$에 대한 $10$의 보수는?
  - $100 - 33 = 67$이다.
- $2$진수에서, 1010에 대한 $1$의 보수는?
  - 1111 - 1010 = 0101이다.
  - 이것은 0과 1의 반전이다.
- $2$진수에서, 1010에 대한 $2$의 보수는?
  - 10000 - 1010 = 0110이다.
  - 이것은 $1$의 보수 $+ 1$이다.
  - 즉, 0과 1을 반전 시키고 $1$을 더하면 된다.

컴퓨터에서 음수 양수를 구별 하기위해 최상위 비트(MSB; Most significant bit) 를 부호비트로 사용한다.
- $1$은 0001이므로 $-1$는 1001가 되겠다.
- 그 둘을 빼면?
  - $0$이어야 하는데 1010이 나오는 문제가 있다.
그러면 $1$의 보수법을 사용해서 음수를 표현하면 어떨까?
- 0과 1를 반전시켜서 음수를 표현하면 되겠다.
- $1$인 0001과 $-1$인 1110을 더하면?
  - 1111이 나온다.
  - $1$의 보수는 $+0$인 0000과 $-0$인 1111의 두 가지 $0$이 존재한다는 문제점이 있다.
그래서 $2$의 보수법을 사용해서 음수를 표현한다.
- 0과 1을 바꾼다음 $1$을 더해서 음수를 표현하면 되겠다.
- $1$인 0001과 $-1$인 1111을 더하면?
  - 10000이 나온다.
- 여기서 MSB가 1이지만, 범위를 벗어났기 때문에 결과적으로 $0$인 0000이 된다.
결과적으로, 음수를 나타내려면, 0과 1을 반전시켜서 $1$을 더한 수에다가 MSB에 1을 붙이면 되겠다.

Image Source

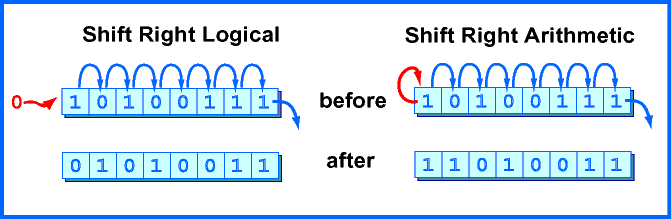
논리 우측 시프트와 산술 우측 시프트 #

Image Source

논리 우측 시프트(Logical right shift)
- 비트를 오른쪽으로 옮긴 후, MSB에 0을 넣는다.
- >>> 연산과 같다.
산술 우측 시프트(Arithmetic right shift)
- 비트를 오른쪽으로 옮기지만, MSB 비트는 변하지 않는다.
- >> 연산과 같다.
- 이것은 대략 값을 $2$로 나눈 것과 같은 결과이다.

기본 비트 조작 예시 #

#include <iostream>
#include <bitset>
using namespace std;

const int bitSize = 4;

void Printer(int num, int mask, int result)
{
  cout << "\t원래 숫자 : \t" << bitset<bitSize>(num) << endl;
  cout << "\t마스크    : \t" << bitset<bitSize>(mask) << endl;
  cout << "\t결과 숫자 : \t" << bitset<bitSize>(result) << endl;
}

bool IsBitOne(int num, int i)
{
  int mask = 1 << i;
  
  cout << i << " 번째 자리 수가 1인가? : " << endl;
  Printer(num, mask, num & mask);
  
  return (num & mask) != 0;
}

int SetBitOne(int num, int i)
{
  int mask = 1 << i;
  
  cout << i << " 번째 자리 수를 1로 만들기 : " << endl;
  Printer(num, mask, num | mask);

  return num | mask;
}

int SetBitZero(int num, int i)
{
  int mask = ~(1 << i);
  
  cout << i << " 번째 자리 수를 0으로 만들기 : " << endl;
  Printer(num, mask, num & mask);

  return num & mask;
}

int SetBitZeroAfterIndex(int num, int i)
{
  int mask = (1 << i + 1) - 1;
  
  cout << i << " 번째 자리 이후(i 자리 제외)를 모두 0으로 만들기 : " << endl;
  Printer(num, mask, num & mask);

  return num & mask;
}

int SetBitZeroBeforeIndex(int num, int i)
{
  int mask = ~((1 << i) - 1);
  
  cout << i << " 번째 자리 이전(i 자리 제외)을 모두 0으로 만들기 : " << endl;
  Printer(num, mask, num & mask);

  return num & mask;
}

int UpdateBit(int num, int i, bool setOne)
{
  int value = ((setOne) ? 1 : 0) << i;
  int mask = ~(1 << i);
  int remove = num & mask;
  
  cout << i << " 번째 자리 비트를 " << setOne << "으로 만들기 : " << endl;
  Printer(num, mask, remove);
  cout << "\t숫자 입력 : \t" << bitset<bitSize>(remove | value) << endl;

  return remove | value;
}

int main() 
{
  int num = 7; // 숫자       : 1 1 1 
  int i = 1;   // 몇 번째 자리 : 2 1 0
  
  IsBitOne(num, i);
  SetBitOne(num, i);
  SetBitZero(num, i);
  SetBitZeroAfterIndex(num, i);
  SetBitZeroBeforeIndex(num, i);
  UpdateBit(num, i, 0);
  UpdateBit(num, i, 1);
  
  return 0;
}

1 번째 자리 수가 1인가? : 
    원래 숫자 :     0111
    마스크    :     0010
    결과 숫자 :     0010
1 번째 자리 수를 1로 만들기 : 
    원래 숫자 :     0111
    마스크    :     0010
    결과 숫자 :     0111
1 번째 자리 수를 0으로 만들기 : 
    원래 숫자 :     0111
    마스크    :     1101
    결과 숫자 :     0101
1 번째 자리 이후(i 자리 제외)를 모두 0으로 만들기 : 
    원래 숫자 :     0111
    마스크    :     0011
    결과 숫자 :     0011
1 번째 자리 이전(i 자리 제외)을 모두 0으로 만들기 : 
    원래 숫자 :     0111
    마스크    :     1110
    결과 숫자 :     0110
1 번째 자리 비트를 0으로 만들기 : 
    원래 숫자 :     0111
    마스크    :     1101
    결과 숫자 :     0101
    숫자 입력 :     0101
1 번째 자리 비트를 1으로 만들기 : 
    원래 숫자 :     0111
    마스크    :     1101
    결과 숫자 :     0101
    숫자 입력 :     0111

수학 및 논리 퍼즐 #

소수 #

모든 자연수는 소수의 곱으로 나타낼 수 있다는 법칙이 있다.
- 따라서 $x/y$로 나눌 수 있으려면,
- $x$에 대한 소수의 곱 $\supset$ $y$에 대한 소수의 곱이 되어야 한다.
- $x = 2^{a_0} \times 3^{a_1} \times 5^{a_2} \times 7^{a_3} …$
- $y = 2^{b_0} \times 3^{b_1} \times 5^{b_2} \times 7^{b_3}…$
- $a_i \geq b_i$
그렇다면 $x$와 $y$의 최대공약수(Greatest common divisor) 는?
- $gcd(x, y) = 2^{min(a_0, b_0)} \times 3^{min(a_1, b_1)} \times 5^{min(a_2, b_2)}$
그렇다면 $x$와 $y$의 최소공배수(Least Common multiple) 는?
- $lcm(x, y) = 2^{max(a_0, b_0)} \times 3^{max(a_1, b_1)} \times 5^{max(a_2, b_2)}$

어떤 수가 소수인지 판별하는 법
- 어떤 수가 소수이려면, $1$과 자기자신 말고는 약수가 없어야 한다.
- 소수가 아닌 경우, 가운데 위치한 약수를 중심으로 대칭적으로 약수가 형성된다.
- 예를 들어, $16$의 경우 약수가 $1$, $2$, $4$, $8$, $16$ 이므로 $4$를 중심으로 대칭적으로 약수가 형성됨을 알 수 있다.
- 따라서 어떤 수의 제곱근까지만 약수인지 판별하면 된다.

void IsPrimeNumber(int num)
{
    for (int i = 2; i <= sqrt(num); i++) // num의 제곱근까지만 검사한다. 
    {
        if (num % i != 0) continue;
        return false; // 나누어 떨어지면 소수가 아니다. 
    }

    return true;
}

$1$부터 $N$까지의 모든 소수를 찾는 법 : 에라토스테네스의 체(Sieve of Eratosthenes)

vector<bool> GetPrimeNumbers(int num)
{
    vector<bool> isPrime(num + 1, true);

    for (int i = 2; i < sqrt(num); i++) // num의 제곱근까지만 검사한다. 
    {
        if (isPrime[i] == false) continue; // 아직 처리하지 않은 가장 작은 수를 선택한다

        int mul = 2;
        while(i * mul <= num) // 그 수의 배수를 모두 제거한다 (그 수는 제거하면 안 됨)
        {
            isPrime[i * mul] = false;
            mul++;
        }
    }

    return isPrime;
}

확률 #

Image Source

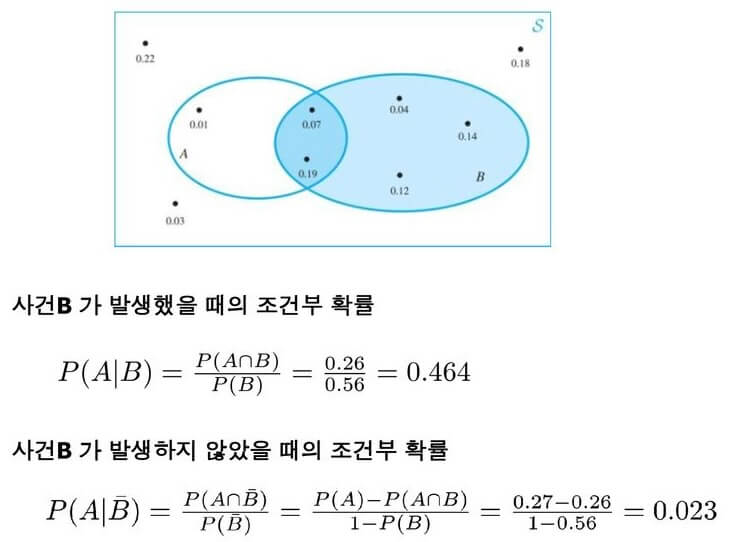
조건부 확률
- $P(A | B)$는 $B$ 사건이 발생했을 때, $A$가 일어날 확률이다.
- 즉, $B$를 사건 전체로 보고 $B$ 중에서 $A$인 부분이다.
- 이것을 사건 $B$에 대한 $A$의 조건부 확률이라고 한다.
- $$ P(A | B) = \frac{ P(A \cap B) }{ P(B) } $$
- $$ P(A \cap B) = P(A | B) P(B) $$

교집합의 확률
- $1$부터 $10$까지의 수 중에서 하나를 뽑을 때, 짝수이면서 $5$ 이하의 수를 뽑을 확률은 어떻게 될까?
- $$ P(짝수 \cap 5이하) = P(짝수 | 5이하) P(5이하) $$
- $$ P(짝수 \cap 5이하) = \frac{2}{5} * \frac{1}{2} = \frac{1}{5}$$

베이즈 정리(Bayes’ Theorem)
- 조건부 확률을 다음과 같이 정리할 수 있겠다.
- $$ P(A \cap B) = P(A | B) P(B) = P(B | A) P(A) $$
- $$ P(A | B) = \frac{ P(B \cap A)P(A) }{ P(B) } $$

합집합의 확률
- $A$ 사건 혹은 $B$ 사건이 벌어질 확률은?
- $$ P(A \cup B) = P(A) + P(B) - P(A \cap B) $$
- $1$부터 $10$까지의 수 중에서 하나를 뽑을 때, 짝수이거나 $5$ 이하의 수를 뽑을 확률은 어떻게 될까?
- $$ P(짝수 \cup 5이하) = P(짝수) + P(5이하) - P(짝수 \cap 5이하)$$
- $$ P(짝수 \cup 5이하) = \frac{1}{2} + \frac{1}{2} - \frac{1}{5} = \frac{4}{5}$$

독립 사건(independent event)
- $A$와 $B$가 서로 아무런 영향을 미치지 않는 사건을 말한다.
- $ P(A \cap B) = 0 $, $ A \cup B = U $
- 예를 들면, $A$ 라는 사람이 공부를 하는 것과 $B$ 라는 사람이 음식을 먹는 것은 독립적인 사건이다. 서로에게 아무런 영향이 없다.
- 따라서 다음과 같은 공식이 성립한다.
- $$ P(A | B) = P(A | B^c) = P(A) $$
- 이것을 조건부 확률 공식에 대입하면 다음과 같다.
- $$ P(A \cap B) = P(A) P(B) $$

상호 배타적 사건(mutually exclusive event)
- 어떤 한 사건이 일어나면 다른 사건은 일어날 수 없는 경우이다.
- $ P(A \cap B) = 0 $, $ (A, B) \subset C $
- $A$와 $B$는 $C$라는 집단 안에 소속되어 있지만 서로 공통적인 부분은 없다는 뜻이다.
- 예를 들면, 남성과 여성은 상호배타적이다. 남성과 여성은 둘 다 ‘인간’이라는 카테고리에 포함되지만 서로 다르기 때문이다.
- $P(A \cap B) = 0$이므로 다음과 같다.
- $$ P(A \cup B) = P(A) + P(B) $$

독립 사건과 상호 배타적 사건은 서로 다른 개념이며, 독립 사건이면서 상호 배타적 사건인 경우는 존재하지 않는다.

재귀와 동적 프로그래밍 #

재귀적 해법 #

해당 문제가 재귀 문제인지 아는 방법?
- 해당 문제를 작은 크기의 부분문제(Subproblem) 로 만들 수 있는지 본다.

(1) 하향식 접근법(Top-down approach)
- 문제를 어떻게 하면 부분문제로 나눌 수 있는지 생각해본다. 부분문제끼리 겹치지 않아야 한다.
(2) 상향식 접근법(Bottom-up approach)
- 간단한 것부터 풀이를 시작해서, 이전에 풀었던 사례를 확장하여 다음 풀이를 찾는다.
- 예를 들면, 원소 하나를 갖는 리스트에서 시작하여, 두 개, 세 개 늘려가며 풀이법을 찾는다.
(3) 반반 접근법(Half-and-half approach)
- 데이터를 절반으로 나누는 방법이다.
- 예를 들면, 이진 탐색이나 병합 정렬이 있겠다.

재귀적 해법 vs. 순환적 해법
- 재귀 호출이 한 번 발생할 때마다 스택에 새로운 층(layer)을 추가해야 하므로, 공간 효율성이 나빠질 수 있다.
- 모든 재귀적(recursive) 알고리즘은 순환적(iterative) 으로 구현이 가능하다.
- 하지만 때로 순환적 알고리즘은 코드가 복잡해지므로, 잘 절충해서 선택해야겠다.

동적 프로그래밍 #

동적 프로그래밍이란?
- 부분문제를 찾아서, 재귀나 반복문을 사용해서 푸는데, 현재 결과를 캐시에 저장해서 연산 속도를 비약적으로 높인다.

Image Source

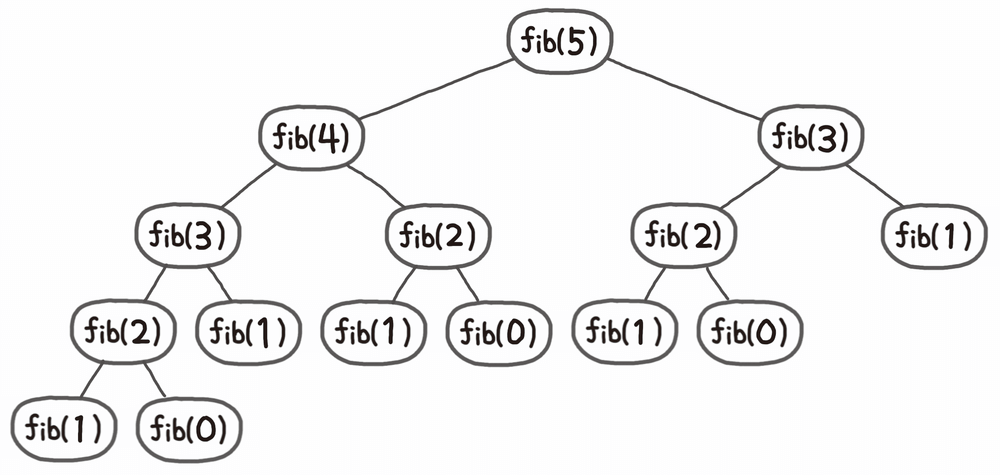
예를 들면, 바로 앞 두 항의 합을 구하는 피보나치 수(Fibonacci number) 가 있다.
- 간단하게 구현한 아래 코드의 경우 재귀 트리를 참고하면, 계속 2개의 자식으로 분기되므로 $O(2^n)$의 시간복잡도가 걸린다.

int GetFibonacci(int x)
{
    if (x == 1 || x == 2) return 1;
    return GetFibonacci(x - 1) + GetFibonacci(x - 2);
}

(1) 하향식 동적 프로그래밍(메모이제이션)
- 재귀 트리를 살펴보면, 중복되는 노드들이 있다.
- 이 값들을 저장했다가 사용하면 시간복잡도를 $O(n)$으로 만들 수 있겠다.

int GetFibonacci(int x, vector<int>& d)
{
    if (x == 1 || x == 2) return 1;

    if (d[x] != 0) return d[x]; // 이미 계산한 적 있는 문제라면 그대로 반환

    d[x] = GetFibonacci(d, x - 1) + GetFibonacci(d, x - 2); 
    return d[x];
}

(2) 상향식 동적 프로그래밍
- 초기 사례인 fib(0)과 fib(1)을 구하고 이것을 이용해 fib(2)를 계산하며 점점 올라가는 방식이다.

int GetFibonacci(int x, vector<int>& d)
{
    d[1] = 1;
    d[2] = 1;

    for (int i = 3; i <= x; i++)
        d[i] = d[i - 1] + d[i - 2];

    return d[x];
}

References #

코딩 인터뷰 완전 분석