[Algorithm] 자료구조 - 그래프

Table of Contents

그래프의 종류 #

그래프
- 노드 간의 네트워크 구조이다.
- 노드와 노드를 연결하는 간선(edge)를 모아 놓은 것이다.

그래프의 종류
- 방향성이 있는가?
  - 무방향, 일방향, 양방향
- 모든 노드가 연결되어 있는가?
  - 이것을 연결 그래프(connected graph)라고 한다.
- 가중치가 있는가?

그래프를 표현하는 방법 #

표현 방법	시간 복잡도	공간 복잡도
인접 리스트	$O(V)$	$O(E)$
인접 행렬	$O(1)$	$O(V^2)$

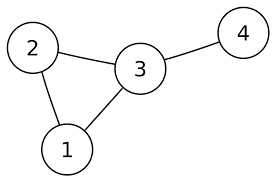
인접 리스트 #

Adjacency list
- (기준노드)배열 or 해시 테이블
- + (기준 노드에 연결된 노드들)배열 or 동적 가변 크기 배열 or 연결리스트

1: 2, 3
2: 1, 3 
3: 1, 2, 4
4: 3

인접 행렬 #

Adjacency matrix
- $n$ x $n$ bool 행렬이다.
- 만약 matrix[i][j]가 true라면 i에서 j로의 간선이 있다는 의미이다.

  |  0    1    2    3    4
----------------------------
0 |  0    0    0    0    0    
1 |  0    0    1    1    0 
2 |  0    1    0    1    0
3 |  0    1    1    0    1
4 |  0    0    0    1    0

그래프 탐색 알고리즘 #

깊이 우선 탐색(DFS) #

Depth-first search
- 끝까지 가본 후에 갈 길이 없으면, 스택에서 꺼내어 다시 끝까지 간다.
- 모든 노드를 방문하고자 할 때 더 선호된다.

#include <iostream>
using namespace std;

const int NODE_MAX = 9;
const int START_NODE = 1;

// graph는 인접 리스트 형태이다.
vector<int> graph[NODE_MAX];
bool visited[NODE_MAX];

void DFS(int node)
{
  // 해당 노드를 방문한다.
  visited[node] = true;
  cout << node << " ";

  // 해당 노드와 연결된 노드들을 방문해간다.
  for (int i = 0; i < graph[node].size(); i++)
  {
      int curNode = graph[node][i];
      if (true == visited[curNode]) continue;
      
      // 연결된 노드 중에 방문하지 않은 노드가 있다면 방문한다.
      DFS(curNode);
  }
}

int main()
{
    //... 그래프 간선 정보 입력받기 ...
    
    DFS(START_NODE);
}

너비 우선 탐색(BFS) #

Breadth-first search
- 인접 노드를 모두 방문하고, 큐에서 꺼내어 다시 모두 방문한다.
- 최단 경로 혹은 임의의 경로를 찾고 싶을 때 더 빠르다.

#include <iostream>
#include <queue>
using namespace std;

const int NODE_MAX = 9;
const int START_NODE = 1;

// graph는 인접 리스트 형태이다.
vector<int> graph[NODE_MAX];
bool visited[NODE_MAX];
    
void BFS(int startNode)
{
    queue<int> q; // 큐를 사용한다.
    
    q.push(startNode); // 첫 노드
    visited[startNode] = true;

    while (false == q.empty())
    {
        // 큐에서 하나를 꺼내 방문한다.
        int curNode = q.front();
        q.pop();
        cout << curNode << " ";
        
        // 해당 노드와 연결된 노드들 중에 방문하지 않은 노드가 있다면 모두 큐에 넣는다.
        for (int i = 0; i < graph[curNode].size(); i++)
        {
            int nextNode = graph[curNode][i];
            if (true == visited[nextNode]) continue;

            q.push(nextNode);
            visited[nextNode] = true;
        }
    }
}

int main()
{
    //... 그래프 간선 정보 입력받기 ...

    BFS(START_NODE);
}

(3) 양방향 탐색(Bidirectional search)
- 출발지와 도착지 사이에 최단 경로를 찾을 때 사용된다.
- 출발지와 도착지 두 노드에서 동시에 BFS를 한 뒤, 충돌하는 경우에 경로를 찾는다.

최단 경로 알고리즘 #

	다익스트라(Dijkstra)	플로이드 워셜(Floyd Warshall)
조건	음의 간선이 없어야 한다
결과	하나의 노드에서 모든 노드로 가는 최단거리	모든 노드에서 모든 노드로 가는 최단거리
표현	인접 리스트	인접 행렬
방법	`A까지 거리 + A~B 거리 < B까지 거리` 이면 갱신	`A~B 최단거리 = min(A~B, A~K~B)`
시간 복잡도	우선순위 큐 사용 시, $O(E \log V)$	$O(V^3)$

다익스트라 #

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

const int INF = 1e9;
const int NODE_MAX = 100001;
const int START_NODE = 1;

// graph는 인접 리스트 형태이며, cost정보가 추가되었다.
vector<pair<int, int>> graph[NODE_MAX]; // graph[from] = { to, cost }
int costs[NODE_MAX];

int nodeNum, edgeNum;

void Dijkstra(int startNode)
{
    // 우선순위 큐를 사용하면 더 빠르다.
    priority_queue<pair<int, int>> pq; // { -cost, from }

    pq.push({ 0, startNode }); // 첫 노드
    costs[startNode] = 0;
    
    while(false == pq.empty())
    {
        // 가장 짧은 거리의 노드를 뺀다.
        int from = pq.top().second;
        int fromCost = -pq.top().first;
        pq.pop();

        if (costs[from] < fromCost) return;

        // 해당 노드와 연결된 노드들 중에
        for (int i = 0; i < graph[from].size(); i++)
        {
            int to = graph[from][i].first;
            int toCost = graph[from][i].second;
            if (fromCost + toCost >= costs[to]) continue; // A까지 총거리 + A~B 거리를, B까지의 총거리와 비교해서 더 짧다면
            
            // 갱신하고 우선순위 큐에 넣는다.
            costs[to] = fromCost + toCost;
            pq.push({ -costs[to], to }); // -를 붙여서 값이 적은 순으로 우선순위가 높게 한다.
        }
    }
}

int main()
{
    cin >> nodeNum >> edgeNum;
    
    // (입력)
    for (int i = 0; i < edgeNum; i++)
    {
        int from, to, cost;
        cin >> from >> to >> cost;
        graph[from].push_back({ to, cost });
    }

    // 최단 거리 테이블을 모두 무한으로 초기화
    fill(costs, costs + NODE_MAX, INF);
    
    Dijkstra(START_NODE);
        
    // (출력)
    for (int i = 1; i < nodeNum + 1; i++)
        cout << costs[i] << " ";
}

플로이드 워셜 #

#include <iostream>
#include <vector>
using namespace std;

const int INF = 1e9;
const int NODE_MAX = 501;

// graph는 인접 행렬 형태이다.
int graph[NODE_MAX][NODE_MAX];

int nodeNum, edgeNum;

void FloydWarshall()
{
    for (int k = 1; k < nodeNum + 1; k++)
        for (int a = 1; a < nodeNum + 1; a++)
            for (int b = 1; b < nodeNum + 1; b++)
                graph[a][b] = min(graph[a][k] + graph[k][b], graph[a][b]);
}

int main()
{
    cin >> nodeNum >> edgeNum;
    
    // 최단 거리 테이블을 모두 무한으로 초기화
    for (int i = 0; i < NODE_MAX; i++)
        fill(graph[i], graph[i] + NODE_MAX, INF);
    
    // 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
    for (int a = 1; a < nodeNum + 1; a++)
       for (int b = 1; b < nodeNum + 1; b++)
           if (a == b)
               graph[a][b] = 0;

    // (입력)
    for (int i = 0; i < edgeNum; i++)
    {
        int from, to, cost;
        cin >> from >> to >> cost;
        graph[from][to] = cost;
    }
    
    FloydWarshall();
    
    // (출력)
    for (int i = 1; i < nodeNum + 1; i++)
    {
        for (int j = 1; j < nodeNum + 1; j++)
            cout << graph[i][j] << " ";
        cout << endl;
    }
}

벨만-포드 #

다익스트라는 음의 간선을 처리할 수 없지만, 벨만-포드는 처리할 수 있다.
- 대신 시간 복잡도가 느리다.
- 따라서 음의 간선이 있다면 벨만-포드를,
- 음의 간선이 없다면 다익스트라를 사용한다.

	다익스트라(Dijkstra)	벨만-포드(Bellman-Ford)
조건	음의 간선이 없어야 한다	음의 간선도 처리할 수 있다
결과	하나의 노드에서 모든 노드로 가는 최단거리	하나의 노드에서 모든 노드로 가는 최단거리
방법	방문하지 않은 노드 중에서 최단 거리가 가장 가까운 노드만을 방문한다	매 단계마다 모든 간선을 전부 확인하면서 모든 노드간의 최단 거리를 구해나간다
시간 복잡도	우선순위 큐 사용 시, $O(E \log V)$	$O(\|V\|\|E\|)$

#include <iostream>
#include <vector>
using namespace std;

struct Edge
{
    int from;
    int to;
    int cost;
};

const int INF = 1e9;
const int NODE_MAX = 100001;
const int START_NODE = 1;

vector<Edge> edges;
int costs[NODE_MAX];

int nodeNum, edgeNum;

bool BellmanFord(int startNode)
{
    // 시작 노드까지의 거리는 0
    costs[startNode] = 0;
    
    // 정점의 횟수만큼
    for (int i = 0; i < nodeNum; i++)
    {
        // 모든 간선을 살펴본다.
        for (int j = 0; j < edgeNum; j++)
        {
            int from = edges[j].from;
            int to = edges[j].to;
            int cost = edges[j].cost;
            
            if (costs[from] == INF) continue;
            if (costs[from] + cost >= costs[to]) continue;
            
            // 새로운 값이 더 작으면 갱신
            costs[to] = costs[from] + cost;
            
            // n번째 라운드에서도 값이 갱신된다면 음수 순환이 존재한다.
            if (i == nodeNum - 1) return true;
        }
    }
    
    return false;
}

int main()
{
    cin >> nodeNum >> edgeNum;
    
    // (입력)
    for (int i = 0; i < edgeNum; i++)
    {
        int from, to, cost;
        cin >> from >> to >> cost;
        edges.push_back({ from, to, cost });
    }

    // 최단 거리 테이블을 모두 무한으로 초기화
    fill(costs, costs + NODE_MAX, INF);
    
    bool negative_cycle = BellmanFord(START_NODE);
    
    // (출력)
    if (true == negative_cycle)
    {
        cout << -1 << endl;
        return 0;
    }
    
    for (int i = 1; i < nodeNum + 1; i++)
        cout << costs[i] << " ";
    cout << endl;
}

A* 알고리즘 #

주어진 출발 노드에서부터 목표 노드까지 가는 최단 경로를 찾아내는 알고리즘이다.
- 출발 노드와 목적지 노드가 명확히 주어진다.
- 다익스트라와 비슷하나, 휴리스틱(Heuristics) 이라는 추정값을 이용해서 최단거리를 구해나간다는 점이 다르다.

각 단계에서 노드를 평가하는 방법은 다음과 같다.
- $ f(n) = g(n) + h(n)$
- $g(n)$ : 출발 노드에서부터 노드 $n$까지의 경비값
- $h(n)$ : 노드 $n$에서부터 목표 노드까지의 추정된 경비값
그리드 맵에서의 휴리스틱 $h(n)$은 다음과 같이 구할 수 있다.
- 4방향 이동 : 맨하튼 거리
- 8방향 이동 : Diagonal 거리
- 어느 방향이든 이동 : 유클리드 거리
- 참고 사이트

그리드 맵에서 8방향 이동 시 A* 알고리즘으로 최단 경로를 구하는 코드

#include <iostream>
#include <iomanip>
#include <vector>
#include <queue>
using namespace std;

const int INF = 1e9;
const int MAX = 100;

struct Pos
{
    int x, y;
};

struct NodeData
{
    int g, h;
    Pos prev; // 이전 노드 값 -> 경로 추적을 위해 저장
    
    NodeData()
    {
        g = INF;
        h = INF;
        prev = {0, 0};
    }
    
    int GetF()
    {
        return g + h;
    }
};

const int DIR_LENGTH = 8;
const Pos DIR[DIR_LENGTH] = {{0, -1}, {1, -1}, {1, 0}, {1, 1}, {0, 1}, {-1, 1}, {-1, 0}, {-1, -1}};

const int DISTANCE = 10;
const int DIAGONAL_DISTANCE = 14;

bool map[MAX][MAX];

int ySize, xSize;
NodeData result[MAX][MAX];

int GetDistance(Pos from, Pos to)
{
    int xDis = abs(from.x - to.x);
    int yDis = abs(from.y - to.y);
    
    int min = (xDis < yDis) ? xDis : yDis;
    int max = (xDis < yDis) ? yDis : xDis;
                    
    // 8방향 이동 : Diagonal 거리를 구한다.
    // x와 y의 갭(max - min)만큼 평행으로 이동(DISTANCE)하고,
    // 짧은 쪽(min)으로 대각선으로 이동(DIAGONAL_DISTANCE)한다.
    return (max - min) * DISTANCE + min * DIAGONAL_DISTANCE;
}

void AStar(Pos start, Pos des)
{
    // 시작노드에서 시작노드까지의 거리 0
    // 시작노드에서 목적지노드까지의 거리 H
    result[start.x][start.y].g = 0;
    result[start.x][start.y].h = GetDistance(start, des);
    result[start.x][start.y].prev = start;
    
    priority_queue<pair<int, pair<int, int>>> pq; // { 우선순위의 기준이 되는 F값, { x, y } }

    pq.push({ -result[start.x][start.y].GetF(), { start.x, start.y } });
                
    while (!pq.empty())
    {
        Pos cur = { pq.top().second.first, pq.top().second.second };
        int curF = -pq.top().first;
        pq.pop();

        // 목적지에 도달했다면 끝내기
        if (cur.x == des.x && cur.y == des.y) break;
            
        // 기존의 F값보다 < 현재 노드의 F값이 더 크면 (더 좋은(짧은) 거리값이 아니면) 필요 없다
        if (result[cur.x][cur.y].GetF() < curF) continue;

        for (int i = 0; i < DIR_LENGTH; ++i)
        {
            Pos next = { cur.x + DIR[i].x, cur.y + DIR[i].y };

            if (next.x < 0 || next.y < 0 || ySize <= next.x || xSize <= next.y) continue;
            if (map[next.x][next.y] == INF) continue;
            
            // 노드 next의 G값 = 이전노드 cur의 G값 + 이전노드와 next의 거리
            // 노드 next의 F값 = G값 + 목적지노드와 next의 거리(H)
            int nextG = result[cur.x][cur.y].g + GetDistance(cur, next);
            int nextH = GetDistance(next, des);
            
            if (result[next.x][next.y].GetF() < nextG + nextH) continue;
            
            result[next.x][next.y].g = nextG;
            result[next.x][next.y].h = nextH;
            result[next.x][next.y].prev = cur;
            
            pq.push({ -result[next.x][next.y].GetF(), { next.x, next.y } });
        }
    }
}

void PrintTable(Pos from, Pos to)
{
    printf("시작 노드 : {%d, %d}, 목적지 노드 : {%d, %d}\n", from.x, from.y, to.x, to.y);
    printf("형식 : G + H = F (이전노드x, 이전노드y)\n");
    
    for (int i = 0; i < ySize; i++)
    {
        for (int j = 0; j < xSize; j++)
        {
            if (result[i][j].g != INF)
            {
                printf("%2d+%2d=%2d(%d, %d) ",
                   result[i][j].g, result[i][j].h, result[i][j].GetF(),
                   result[i][j].prev.x, result[i][j].prev.y);
            }
            else
            {
                cout << setw(15) << "";
            }
        }
        cout << endl;
    }
    cout << endl;
}

void PrintPath(Pos from, Pos to)
{
    // 경로 출력을 위해 목적지부터 되돌아가며 path에 경로 넣기
    vector<Pos> path;
    
    path.push_back(to);
    Pos cur = result[to.x][to.y].prev;
    
    while (1)
    {
        path.push_back(cur);
        if (cur.x == from.x && cur.y == from.y) break;
            
        cur = result[cur.x][cur.y].prev;
    }
    
    cout << "이동경로 : ";

    for (int i = path.size() - 1; i >= 0; i--)
    {
        cout << "{" << path[i].x << ", " << path[i].y << "}";
        
        if (i != 0) cout << " > ";
    }
    
    cout << endl;
}

int main()
{
    cin >> xSize >> ySize;
    
    // (입력)
    for (int i = 0; i < ySize; i++)
        for (int j = 0; j < xSize; j++)
            cin >> map[i][j];
    
    Pos start = { 0, 0 };
    Pos des = { xSize - 1, ySize - 1 };

    AStar(start, des);
        
    // (출력)
    PrintTable(start, des);
    PrintPath(start, des);
}

위상 정렬 #

	위상 정렬(Topology sort)
조건	사이클이 없는 방향 그래프
설명	방향성에 거스르지 않고 순서대로 정렬하기 인접 리스트를 사용한다
시간 복잡도	모든 노드와 간선을 확인하므로, $O(V + E)$이다

#include <iostream>
#include <queue>
using namespace std;

// BFS를 사용한 방법이다.

const int NODE_MAX = 100001;

// graph는 인접 리스트 형태이다.
vector<int> graph[NODE_MAX];

// 진입차수는 해당 노드로 도착하는 간선의 개수이다.
int indegree[NODE_MAX];

int nodeNum, edgeNum;
vector<int> result;

void TopologySort()
{
    // 큐를 사용한다.
    queue<int> q;

    // 진입차수가 0인 노드를 모두 큐에 넣는다.
    for (int i = 1; i < nodeNum + 1; i++)
        if (indegree[i] == 0)
            q.push(i);

    // 큐가 빌 때까지 계속한다.
    while(false == q.empty())
    {
        // 큐에서 노드를 하나 꺼낸다. 꺼낸 순서가 정렬 결과이다.
        int from = q.front();
        q.pop();
        result.push_back(from);

        // 꺼낸 노드와 연결된 노드의 진입차수를 1씩 감소시킨다.
        for (int i = 0; i < graph[from].size(); i++)
        {
            int to = graph[from][i];
            indegree[to]--;
            
            // 진입차수가 0이 되면 큐에 넣는다.
            if (indegree[to] == 0)
                q.push(to);
        }
    }
}

int main()
{
    cin >> nodeNum >> edgeNum;

    // (입력)
    for (int i = 0; i < edgeNum; i++)
    {
        int from, to;
        cin >> from >> to;
        graph[from].push_back(to);
        
        // 진입 차수 설정하기
        indegree[to] += 1;
    }
    
    TopologySort();
    
    // (출력)
    for (int i = 0; i < result.size(); i++)
        cout << result[i] << ' ';
}

최소 비용 신장트리 알고리즘 #

신장 트리(Spanning tree)
- 모든 노드를 포함하면서, 사이클이 존재하지 않는 부분 그래프.
최소 비용 신장트리(MST; Minimum Spanning Tree) 알고리즘
- 최소한의 비용으로 모든 노드를 연결하는 알고리즘.

크루스칼 알고리즘 #

	크루스칼 알고리즘(Kruskal Algorithm)
조건	가중치가 있는 무방향 그래프
설명	그리디를 사용하여 최소 비용 간선 순으로 사이클이 발생하는지 체크한다
시간 복잡도	간선 정렬 작업이 제일 오래걸리는 부분이므로, $O(E \log E)$이다

#include <iostream>
using namespace std;

struct EdgeData
{
    int a;
    int b;
    int cost;
    
    // 비용이 작은 것이 앞으로 간다.
    bool operator<(EdgeData b)
    {
        return cost < b.cost;
    }
};

const int NODE_MAX = 100001;

vector<EdgeData> edges;
int parent[NODE_MAX];

int nodeNum, edgeNum, result = 0;

int FindParent(int idx)
{
    if (idx != parent[idx])
        parent[idx] = FindParent(parent[idx]);

    return parent[idx];
}

void UnionParent(int a, int b)
{
    a = FindParent(a);
    b = FindParent(b);

    if (a > b) parent[a] = parent[b];
    else       parent[b] = parent[a];
}

void Kruskal()
{
    // 부모 테이블을 자기 자신으로 초기화
    for (int i = 1; i < nodeNum + 1; i++)
        parent[i] = i;
    
    // 간선을 비용에 따라 오름차순으로 정렬한다. E log E의 시간 복잡도가 걸린다.
    sort(edges.begin(), edges.end());
    
    for (int i = 0; i < edges.size(); i++)
    {
        int a = edges[i].a;
        int b = edges[i].b;

        // 연결된 두 노드의 부모노드가 같다면 사이클이므로 제외하고,
        if (FindParent(a) == FindParent(b)) continue;
    
        // 다르다면 포함시킨다 == Union한다.
        UnionParent(a, b);
        result += edges[i].cost;
    }
}

int main()
{
    cin >> nodeNum >> edgeNum;

    // (입력)
    for (int i = 0; i < edgeNum; i++)
    {
        int a, b, cost;
        cin >> a >> b >> cost;
        edges.push_back({ a, b, cost });
    }
    
    Kruskal();

    // (출력)  
    cout << result << endl;
}

그래프의 종류 #

그래프를 표현하는 방법 #

인접 리스트 #

인접 행렬 #

그래프 탐색 알고리즘 #

깊이 우선 탐색(DFS) #

너비 우선 탐색(BFS) #

최단 경로 알고리즘 #

다익스트라 #

플로이드 워셜 #

벨만-포드 #

A* 알고리즘 #

위상 정렬 #

최소 비용 신장트리 알고리즘 #

크루스칼 알고리즘 #

References #